UNIVARIATEプロシジャ

CDFPLOTステートメント

サブセクション

CDFPLOT <variables> < / options>;

CDFPLOTステートメントは、次の定義に従って、変数の観測された累積分布関数(CDF)をプロットします。

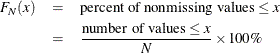
$\begin{eqnarray*} F_{N}(\Emph{x}) & = & \mbox{percent of nonmissing values} \leq \Emph{x} \\ & = & \frac{\mbox{number of values} \leq x}{N} \times 100\% \end{eqnarray*}$

ここでNは非欠損値のオブザベーション数です。CDFは、xが測定値と等しい値になるたびに $\frac{1}{N}$ が垂直方向に急増する、増加型のステップ関数です。CDFは経験累積分布関数(ECDF)とも呼ばれます。

CDFPLOTステートメントは、UNIVARIATEプロシジャ内でいくつでも使用できます。CDFPLOTステートメントの構成要素は次のとおりです。

variables

CDFプロットを作成する変数を指定します。VARステートメントを指定する場合、variablesをそのVARステートメント内にリストする必要があります。そうしない場合、variablesは、入力データセット内にある任意の数値変数になります。variablesのリストを指定しなかった場合、デフォルトではプロシジャによって、VARステートメント内にリストされた各変数のCDFプロットが作成され、VARステートメントが指定されていない場合は、DATA=データセット内の各数値変数のCDFプロットが作成されます。

たとえば、Steelという名前のデータセットに、Length、WidthおよびHeightという、ちょうど3つの数値変数が含まれているとします。次のステートメントは、3つの変数それぞれのCDFプロットを作成します。

proc univariate data=Steel;
   cdfplot;
run;

次のステートメントは、LengthのCDFプロットとWidthのCDFプロットを作成します。

proc univariate data=Steel;
   var Length Width;
   cdfplot;
run;

次のステートメントは、WidthのCDFプロットを作成します。

proc univariate data=Steel;
   var Length Width;
   cdfplot Width;
run;

options

プロットの理論的分布を指定するか、またはプロットに特徴を追加します。1つ以上の変数を指定した場合、各変数に対してoptionsが等しく適用されます。CDFPLOTステートメントのoptionsは、すべてスラッシュ(/)の後に指定します。分布の名前を指定するoptionは、各CDFPLOTステートメントで1つのみ指定できます。その他のoptionsは任意の数だけ指定できます。使用できる分布は表4.2のとおりです。デフォルトでは、このプロシジャは正規分散のプロットを作成します。

表4.2から表4.4は、関数別のCDFPLOT optionsの一覧です。詳細は、オプションのリファレンスおよび共通オプションのリファレンスの各セクションを参照してください。Optionsには次のいずれかを指定します。

1次オプション
2次オプション
一般オプション

分布オプション

表4.2は理論分布を要求するための1次オプションの一覧です。

表4.2: 理論分布の1次オプション

オプション	説明
BETA(beta-options)	2パラメータのベータ分布関数(パラメータ $\theta$ および $\sigma$ は既知であることが前提)をプロット
EXPONENTIAL(exponential-options)	1パラメータの指数分布関数(パラメータ $\theta$ は既知であることが前提)をプロット
GAMMA(gamma-options)	2パラメータのガンマ分布関数(パラメータ $\theta$ は既知であることが前提)をプロット
GUMBEL(Gumbel-options)	Gumbel分布(位置パラメータ $\mu$ および尺度パラメータ $\sigma$ )をプロット
IGAUSS(iGauss-options)	逆ガウス分布(平均 $\mu$ および形状パラメータ $\lambda$ )をプロット
LOGNORMAL(lognormal-options)	2パラメータの対数正規分布関数(パラメータ $\theta$ は既知であることが前提)をプロット
NORMAL(normal-options)	正規分布関数をプロット
PARETO(Pareto-options)	一般化パレート分布(しきい値パラメータ $\theta$ 、尺度パラメータ $\sigma$ 、形状パラメータ $\alpha$ )をプロット
POWER(power-options)	べき関数分布(しきい値パラメータ $\theta$ 、尺度パラメータ $\sigma$ 、形状パラメータ $\alpha$ )をプロット
RAYLEIGH(Rayleigh-options)	レイリー分布(しきい値パラメータ $\theta$ および尺度パラメータ $\sigma$ )をプロット
WEIBULL(Weibull-options)	2パラメータのWeibull分布関数(パラメータ $\theta$ は既知であることが前提)をプロット

表4.3に、分布のパラメータの指定と理論分布関数の表示の制御を行う、2次オプションの一覧を示します。これらのオプションは、分布キーワードの後にかっこで囲んで指定します。たとえば、分布参照線付きの正規確率を要求する場合、次のようなNORMALオプションを指定します。

proc univariate;
   cdfplot / normal(mu=10 sigma=0.5 color=red);
run;

COLOR=オプションは曲線の色を指定し、MU= / SIGMA= normal-optionsは分布関数のパラメータ $\mu = 10$ および $\sigma = 0.5$ を指定します。これらのパラメータを指定しなかった場合、最尤推定値が計算されます。

表4.3: 分布に関する2次オプション

オプション	説明
すべての分布で使用されるオプション
COLOR=	理論分布関数の色を指定
L=	理論分布関数の線の種類を指定
W=	理論分布関数の幅を指定
beta-options
ALPHA=	ベータ分布関数の1番目の形状パラメータ $\alpha$ を指定
BETA=	ベータ分布関数の2番目の形状パラメータ $\beta$ を指定
SIGMA=	ベータ分布関数の尺度パラメータ $\sigma$ を指定
THETA=	ベータ分布関数のしきい値パラメータ $\theta$ を指定
exponential-options
SIGMA=	指数分布関数の尺度パラメータ $\sigma$ を指定
THETA=	指数分布関数のしきい値パラメータ $\theta$ を指定
gamma-options
ALPHA=	ガンマ分布関数の形状パラメータ $\alpha$ を指定
ALPHADELTA=	連続推定値 $\alpha$ の変化を指定(その値で $\hat{\alpha }$ のNewton-Raphson近似が終了)
ALPHAINITIAL=	$\alpha$ の初期値(Newton-Raphson近似が $\hat{\alpha }$ の場合)を指定
MAXITER=	Newton-Raphson近似が $\hat{\alpha }$ の場合の反復の最大数を指定
SIGMA=	ガンマ分布関数の尺度パラメータ $\sigma$ を指定
THETA=	ガンマ分布関数のしきい値パラメータ $\theta$ を指定
Gumbel-options
MU=	Gumbel分布関数の位置パラメータ $\mu$ を指定
SIGMA=	Gumbel分布関数の尺度パラメータ $\sigma$ を指定
iGauss-options
LAMBDA=	逆ガウス分布関数の形状パラメータ $\lambda$ を指定
MU=	逆ガウス分布関数の平均 $\mu$ を指定
lognormal-options
SIGMA=	対数正規分布関数の形状パラメータ $\sigma$ を指定
THETA=	対数正規分布関数のしきい値パラメータ $\theta$ を指定
ZETA=	対数正規分布関数の尺度パラメータ $\zeta$ を指定
normal-options
MU=	正規分布関数の平均値 $\mu$ を指定
SIGMA=	正規分布関数の標準偏差 $\sigma$ を指定
Pareto-options
ALPHA=	一般化パレート分布関数の形状パラメータ $\alpha$ を指定
SIGMA=	一般化パレート分布関数の尺度パラメータ $\sigma$ を指定
THETA=	一般化パレート分布関数のしきい値パラメータ $\theta$ を指定
power-options
ALPHA=	べき関数分布の形状パラメータ $\alpha$ を指定
SIGMA=	べき関数分布の尺度パラメータ $\sigma$ を指定
THETA=	べき関数分布のしきい値パラメータ $\theta$ を指定
Rayleigh-options
SIGMA=	レイリー分布関数の尺度パラメータ $\sigma$ を指定
THETA=	レイリー分布関数のしきい値パラメータ $\theta$ を指定
2次Weibull-options
C=	Weibull分布関数の形状パラメータcを指定
ITPRINT	反復履歴とオプティマイザの詳細に関するテーブルを要求
MAXITER=	Newton-Raphson近似が $\hat{c}$ の場合の反復の最大数を指定
SIGMA=	Weibull分布関数の尺度パラメータ $\sigma$ を指定
THETA=	Weibull分布関数のしきい値パラメータ $\theta$ を指定

一般オプション

表4.4はCDFプロットを拡張するための一般オプションの要約です。

表4.4: 一般グラフオプション

オプション	説明
一般グラフオプション
HREF=	水平軸に垂直な参照線を指定
HREFLABELS=	HREF=で指定した参照線のラベルを指定
HREFLABPOS=	HREF=で指定した参照線のラベルの位置を指定
NOECDF	経験(観測された)分布関数のプロットを抑制
NOHLABEL	水平軸のラベルを抑制
NOVLABEL	垂直軸のラベルを抑制
NOVTICK	垂直軸の目盛りおよび目盛りラベルを抑制
STATREF=	要約統計量の値に参照線を指定
STATREFLABELS=	STATREF=で指定した参照線のラベルを指定
STATREFSUBCHAR=	STATREFLABELS=ラベルに統計値を表示するための置き換え文字を指定
VAXISLABEL=	垂直軸にラベルを指定
VREF=	垂直軸に垂直な参照線を指定
VREFLABELS=	VREF=で指定した参照線のラベルを指定
VREFLABPOS=	VREF=で指定した参照線のラベルの位置を指定
VSCALE=	垂直軸のスケールを指定
従来的なグラフ出力のオプション
ANNOTATE=	ANNOTATEのデータセットを指定
CAXIS=	軸の色を指定
CFRAME=	枠の色を指定
CHREF=	HREF=で指定した参照線の色を指定
CSTATREF=	STATREF=で指定した参照線の色を指定
CTEXT=	テキストの色を指定
CVREF=	VREF=で指定した参照線の色を指定
DESCRIPTION=	グラフカタログメンバに対する説明を指定
FONT=	テキストフォントを指定
HAXIS=	水平軸のAXISステートメントを指定
HEIGHT=	枠外の領域で使用されるテキストの高さを指定
HMINOR=	水平軸の小目盛りの数を指定
INFONT=	枠領域内のテキストに対してソフトウェアフォントを指定
INHEIGHT=	枠領域内のテキストの高さを指定
LHREF=	HREF=で指定した参照線の種類を指定
LSTATREF=	STATREF=で指定した参照線の種類を指定
LVREF=	VREF=で指定した参照線の種類を指定
NAME=	グラフカタログ内のプロットに対して名前を指定
NOFRAME	プロット領域の周囲の枠の表示を抑制
TURNVLABELS	垂直軸のラベルの文字列を縦書きに
VAXIS=	垂直軸のAXISステートメントを指定
VMINOR=	垂直軸の小目盛りの数を指定
WAXIS=	軸と枠の線の太さを指定
ODS Graphics出力のオプション
ODSFOOTNOTE=	プロットに表示するフットノートを指定
ODSFOOTNOTE2=	プロットに表示するセカンダリフットノートを指定
ODSTITLE=	プロットに表示するタイトルを指定
ODSTITLE2=	プロットに表示するセカンダリタイトルを指定
OVERLAY	異なるクラス水準のプロットを重ね合わせる
比較プロットのオプション
ANNOKEY	ANNOTATE=データセットで要求された注釈をキーセルに対してのみ適用
CFRAMESIDE=	行ラベルの枠を塗りつぶす色を指定
CFRAMETOP=	列ラベルの枠を塗りつぶす色を指定
CPROP=	度数のバーの割合の色を指定
CTEXTSIDE=	行ラベルの色を指定
CTEXTTOP=	列ラベルの色を指定
INTERTILE=	比較プロットのタイル間の距離を指定
NCOLS=	比較プロットの列数を指定
NROWS=	比較プロットの列数を指定
その他のオプション
CONTENTS=	CDFプロットグループの目次エントリを指定

オプションのリファレンス

CDFPLOTステートメント特有のオプションの詳細は次のとおりです。すべてのプロットステートメントに共通するオプションの詳細は、共通オプションのリファレンスセクションを参照してください。

ALPHA=value

BETA 、GAMMA 、PARETO 、POWER オプションで要求された分布関数の形状パラメータ $\alpha$ を指定します。ALPHA=オプションは、分布を表すキーワードの後にかっこで囲んで指定します。 $\alpha$ の値を省略すると、最尤推定値が計算されます。例は、BETAおよびGAMMAオプションの項目を参照してください。

BETA<(beta-options )>

CDFプロットに、当てはめたベータ分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ I_{\frac{x - \theta }{\sigma }} (\alpha , \beta ) & \mbox{for }\theta < x < \theta + \sigma \\ 1 & \mbox{for }x \geq \sigma + \theta \end{array} \right.$

ここで、 $I_ y (\alpha , \beta )$ は不完全なベータ関数です。

$\theta =$ 下限しきい値パラメータ(下限端点)
$\sigma =$ 尺度パラメータ $(\sigma >0)$
$\alpha =$ 形状パラメータ $(\alpha >0)$
$\beta =$ 形状パラメータ $(\beta >0)$

ベータ分布の下限はパラメータ $\theta$ で、上限は値 $\theta + \sigma$ です。 $\theta$ および $\sigma$ は、THETA= およびSIGMA= beta-optionsを使用して指定しますが、次のステートメントに示すように、50から75の間の値を取りうるベータ分布を当てはめます。 $\theta$ のデフォルト値は0、 $\sigma$ のデフォルト値は1です。

proc univariate;
   cdfplot / beta(theta=50 sigma=25);
run;

ベータ分布には、2つの形状パラメータ $\alpha$ および $\beta$ があります。これらのパラメータが判明している場合、その値をALPHA= およびBETA= beta-optionsに指定できます。 $\alpha$ および $\beta$ に値を指定しない場合、最尤推定値が計算されます。

BETAオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、BETA分布オプションと共に指定できるオプションの一覧を示します。

BETA=value B=value

BETAオプションで要求したベータ分布関数の2番目の形状パラメータ $\beta$ を指定します。BETA=オプションは、BETAキーワードの後にかっこで囲んで指定します。 $\beta$ の値を省略すると、最尤推定値が計算されます。例は、前のBETAオプションの項目を参照してください。

C=value

WEIBULLオプションで要求したWeibull分布関数の形状パラメータcを指定します。C=オプションは、WEIBULLキーワードの後にかっこで囲んで指定します。c値を指定しない場合、最尤推定値がプロシジャによって計算されます。SHAPE=オプションは、C=オプションの別名として指定できます。

EXPONENTIAL<(exponential-options )> EXP<(exponential-options )>

CDFプロットに、当てはめた指数分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ 1 - \exp \left(-\frac{x - \theta }{\sigma } \right) & \mbox{for }x > \theta \end{array} \right.$

ここで、

$\theta =$ しきい値パラメータ
$\sigma =$ 尺度パラメータ $(\sigma >0)$

パラメータ $\theta$ は最小データ値以下である必要があります。 $\theta$ は、THETA= exponential-optionで指定できます。 $\theta$ のデフォルト値は0です。 $\sigma$ は、SIGMA= exponential-optionで指定できます。デフォルトでは、 $\sigma$ の最尤推定値が計算されます。たとえば、次のステートメントは、 $\theta = 10$ で $\sigma$ が最尤推定値の指数分布を当てはめます。

proc univariate;
   cdfplot / exponential(theta=10 l=2 color=green);
run;

指数曲線の色は緑で、線の種類は2です。

EXPONENTIALオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、EXPONENTIALオプションと共に指定できるオプションの一覧を示します。

GAMMA<(gamma-options)>

CDFプロットに、当てはめたガンマ分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ \frac{1}{\Gamma (\alpha ) \sigma } \int _{\theta }^ x \left(\frac{t-\theta }{\sigma } \right)^{\alpha - 1} \exp \left( -\frac{t - \theta }{\sigma } \right) dt & \mbox{for }x > \theta \end{array} \right.$

ここで、

$\theta =$ しきい値パラメータ
$\sigma =$ 尺度パラメータ $(\sigma >0)$
$\alpha =$ 形状パラメータ $(\alpha >0)$

ガンマ分布のパラメータ $\theta$ は、最小データ値未満である必要があります。 $\theta$ は、THETA= gamma-optionで指定できます。 $\theta$ のデフォルト値は0です。また、ガンマ分布は、形状パラメータ $\alpha$ および尺度パラメータ $\sigma$ を持ちます。これらのパラメータは、ALPHA= およびSIGMA= gamma-optionsで指定できます。デフォルトでは、 $\alpha$ および $\sigma$ の最尤推定値が計算されます。たとえば、次のステートメントは、 $\theta =4$ で、 $\alpha$ および $\sigma$ が最尤推定値のガンマ分布関数を当てはめます。

proc univariate;
   cdfplot / gamma(theta=4);
run;

$\alpha$ の最尤推定値はNewton-Raphson近似を使用して計算されることに注意してください。ALPHADELTA= 、ALPHAINITIAL= 、およびMAXITER= のgamma-optionsが近似を制御します。

GAMMAオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、GAMMAオプションと共に指定できるオプションの一覧を示します。

GUMBEL<(Gumbel-options)>

CDFプロットに、当てはめたGumbel分布(Type 1極値分布とも呼ばれます)関数を表示します。適合CDFの式は次のようになります。

$F(x) = \exp \left( -e^{-(x - \mu )/\sigma } \right)$

$\mu =$ 位置パラメータ $\sigma =$ 尺度パラメータ $(\sigma >0)$

$\mu$ および $\sigma$ の既知の値を指定するには、MU= およびSIGMA= Gumbel-optionsを使用します。デフォルトでは、 $\mu$ および $\sigma$ の最尤推定値が計算されます。

GUMBELオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、GUMBELオプションと共に指定できる2次オプションの一覧を示します。

IGAUSS<(iGauss-options)>

CDFプロットに、当てはめた逆ガウス分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \Phi \left\{ \sqrt {\frac{\lambda }{x}} \left( \frac{x}{\mu } - 1 \right) \right\} + e^{2\lambda /\mu } \Phi \left\{ -\sqrt {\frac{\lambda }{x}} \left( \frac{x}{\mu } + 1 \right) \right\}$

ここで、 $\Phi (\cdot )$ は標準正規累積分布関数です。 $\mu =$ 平均パラメータ $(\mu > 0)$ $\lambda =$ 形状パラメータ $(\lambda >0)$

$\mu$ および $\lambda$ の既知の値を指定するには、MU= およびLAMBDA= iGauss-optionsを使用できます。デフォルトでは、 $\mu$ および $\lambda$ の最尤推定値が計算されます。

IGAUSSオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、IGAUSSオプションと共に指定できる2次オプションの一覧を示します。

LAMBDA=value

IGAUSSオプションで要求した分布関数の形状パラメータ $\lambda$ を指定します。LAMBDA=オプションは、分布を表すキーワードIGAUSSの後にかっこで囲んで指定します。 $\lambda$ の値を省略すると、最尤推定値が計算されます。

LOGNORMAL<(lognormal-options)>

CDFプロットに、当てはめた対数正規分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ \Phi \left( \frac{\log (x-\theta )-\zeta }{\sigma } \right) & \mbox{for }x > \theta \end{array} \right.$

ここで、 $\Phi (\cdot )$ は標準正規累積分布関数であり、各パラメータは次のとおりです。

$\theta =$ しきい値パラメータ
$\zeta =$ 尺度パラメータ
$\sigma =$ 形状パラメータ $(\sigma >0)$

対数正規分布のパラメータ $\theta$ は、最小データ値未満である必要があります。 $\theta$ は、THETA= lognormal-optionで指定できます。 $\theta$ のデフォルト値は0です。また、対数正規分布は、形状パラメータ $\sigma$ および尺度パラメータ $\zeta$ を持ちます。これらのパラメータは、SIGMA= およびZETA= lognormal-optionsで指定できます。デフォルトでは、 $\sigma$ および $\sigma$ の最尤推定値が計算されます。たとえば、次のステートメントは、 $\theta =10$ で、 $\sigma$ および $\zeta$ が最尤推定値のガンマ分布関数を当てはめます。

proc univariate;
   cdfplot / lognormal(theta = 10);
run;

LOGNORMALオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、LOGNORMALオプションと共に指定できるオプションの一覧を示します。

MU=value

GUMBEL 、IGAUSS 、およびNORMAL オプションで要求した理論累積分布関数のパラメータ $\mu$ を指定します。MU=オプションは、分布を表すキーワードの後にかっこで囲んで指定します。逆ガウス分布および正規分布の場合、デフォルト値は標本平均です。 $\mu$ の値を省略すると、最尤推定値が計算されます。例は、NORMALオプションの項目を参照してください。

NOECDF

デフォルトで描画される、変数の観測された分布関数(経験累積分布関数)を抑制します。このオプションを使用すると、データ分布を表示せずに理論CDFプロットを作成できます。NOECDFオプションは、理論分布(NORMALオプションなど)でのみ使用できます。

NORMAL<(normal-options)>

CDFプロットに、当てはめた正規分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left.\begin{array}{ll} \Phi \left( \frac{x - \mu }{\sigma } \right) & \mbox{for }-\infty < x < \infty \end{array} \right.$

ここで、 $\Phi (\cdot )$ は標準正規累積分布関数であり、各パラメータは次のとおりです。

$\mu =$ 平均
$\sigma =$ 標準偏差 $(\sigma >0)$

$\mu$ および $\sigma$ の既知の値を指定するには、MU= およびSIGMA= normal-optionsを次のステートメントに示すように、使用します。

proc univariate;
   cdfplot / normal(mu=14 sigma=.05);
run;

デフォルトでは、 $\mu$ および $\sigma$ の標本平均および標本標準偏差が計算されます。NORMALオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、NORMALオプションと共に指定できるオプションの一覧を示します。

PARETO<(Pareto-options)>

CDFプロットに、当てはめた一般化パレート分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = 1 - { \left( 1 - \frac{\alpha (x - \theta )}{\sigma } \right) }^\frac {1}{\alpha }$

ここで、 $\theta =$ しきい値パラメータ $\sigma =$ 尺度パラメータ $(\sigma >0)$ $\alpha =$ 形状パラメータ

一般パレート分布のパラメータ $\theta$ は、最小データ値未満である必要があります。 $\theta$ は、THETA= Pareto-optionで指定できます。 $\theta$ のデフォルト値は0です。また、一般パレート分布は、形状パラメータ $\alpha$ および尺度パラメータ $\sigma$ を持ちます。これらのパラメータは、ALPHA= およびSIGMA= Pareto-optionsで指定できますデフォルトでは、 $\alpha$ および $\sigma$ の最尤推定値が計算されます。

PARETOオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、PARETOオプションと共に指定できるオプションの一覧を示します。

POWER<(power-options)>

CDFプロットに、当てはめたべき分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ {\left( \frac{x - \theta }{\sigma } \right)}^{\alpha } & \mbox{for }\theta < x < \theta + \sigma \\ 1 & \mbox{for }x \geq \theta + \sigma \end{array} \right.$

ここで、 $\theta =$ 下限しきい値パラメータ(下限端点) $\sigma =$ 尺度パラメータ $(\sigma > 0)$ $\alpha =$ 形状パラメータ $(\alpha > 0)$

べき関数分布の下限はパラメータ $\theta$ で、上限は値 $\theta + \sigma$ です。 $\theta$ および $\sigma$ を指定するには、THETA=およびSIGMA=power-optionsを使用します。 $\theta$ のデフォルト値は0、 $\sigma$ のデフォルト値は1です。

形状パラメータ $\alpha$ の値を指定するには、ALPHA= power-optionを使用します。 $\alpha$ の値を省略すると、最尤推定値が計算されます。

べき関数分布は、2番目の形状パラメータ $\beta = 1$ を持つ、ベータ分布の特殊なケースです。

POWERオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、POWERオプションと共に指定できるオプションの一覧を示します。

RAYLEIGH<(Rayleigh-options)>

CDFプロットに、当てはめたレイリー分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = 1 - e^{-(x - \theta )^2/(2\sigma ^2)}$

ここで、 $\theta =$ しきい値パラメータ $\sigma =$ 尺度パラメータ $(\sigma >0)$

レイリー分布のパラメータ $\theta$ は、最小データ値未満である必要があります。 $\theta$ は、THETA= Rayleigh-optionで指定できます。 $\theta$ のデフォルト値は0です。 $\sigma$ は、SIGMA=Rayleigh-optionで指定できます。デフォルトでは、 $\sigma$ の最尤推定値が計算されます。

RAYLEIGHオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、RAYLEIGHオプションと共に指定できるオプションの一覧を示します。

SIGMA=value | EST

BETA、EXPONENTIAL、GAMMA、LOGNORMAL、NORMAL、WEIBULLオプションで要求した分布関数のパラメータ $\sigma$ を指定します。SIGMA=オプションは、分布を表すキーワードの後にかっこで囲んで指定します。次の表はSIGMA=オプションの使用方法の要約です。

分布オプション	SIGMA=に指定する値	デフォルト値	別名
BETA	尺度パラメータ $\sigma$	1	SCALE=
EXPONENTIAL	尺度パラメータ $\sigma$	最尤推定値	SCALE=
GAMMA	尺度パラメータ $\sigma$	最尤推定値	SCALE=
GUMBEL	尺度パラメータ $\sigma$	最尤推定値
LOGNORMAL	形状パラメータ $\sigma$	最尤推定値	SHAPE=
NORMAL	尺度パラメータ $\sigma$	標準偏差
PARETO	尺度パラメータ $\sigma$	最尤推定値
POWER	尺度パラメータ $\sigma$	1
RAYLEIGH	尺度パラメータ $\sigma$	最尤推定値
WEIBULL	尺度パラメータ $\sigma$	最尤推定値	SCALE=

THETA=value | EST THRESHOLD=value | EST

BETA 、EXPONENTIAL 、GAMMA 、LOGNORMAL 、PARETO 、POWER 、RAYLEIGH 、WEIBULL の各オプションで要求した理論累積分布関数の下限しきい値パラメータ $\theta$ $\theta $を指定します。THETA=オプションは、分布を表すキーワードの後にかっこで囲んで指定します。デフォルト値は0です。

VSCALE=PERCENT | PROPORTION

垂直軸の尺度を指定します。値PERCENTは、データ単位をデータユニットごとのオブザベーションのパーセントに変換します。値PROPORTIONは、データ単位をデータユニットごとのオブザベーションの比率に変換します。デフォルト値はPERCENTです。

WEIBULL<(Weibull-options)>

CDFプロットに、当てはめたWeibull分布関数を表示します。適合CDFの式は次のようになります。

$F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for }x \leq \theta \\ 1 - \exp \left( - \left( \frac{x - \theta }{\sigma } \right)^ c \right) & \mbox{for }x > \theta \end{array} \right.$

ここで、

$\theta =$ しきい値パラメータ
$\sigma =$ 尺度パラメータ $(\sigma >0)$
$\mi{c} =$ 形状パラメータ $(\mi{c} >0)$

パラメータ $\theta$ は最小データ値未満である必要があります。 $\theta$ は、THETA= Weibull-optionで指定できます。 $\theta$ デフォルト値は0です。また、Weibull分布には、形状パラメータcおよび尺度パラメータ $\sigma$ があります。これらのパラメータは、SIGMA= およびC= Weibull-optionsで指定できます。デフォルトでは、cおよび $\sigma$ の最尤推定値が計算されます。たとえば、次のステートメントは、 $\theta =15$ で、 $\sigma$ およびcが最尤推定値のWeibull分布関数を当てはめます。

proc univariate;
   cdfplot / weibull(theta=15);
run;

WEIBULLオプションは、CDFPLOTステートメントに1回だけ指定できます。表4.3に、WEIBULLオプションと共に指定できるオプションの一覧を示します。

ZETA=value

LOGNORMALオプションで要求した対数正規分布関数の尺度パラメータ $\zeta$ の値を指定します。ZETA=オプションは、LOGNORMALキーワードの後にかっこで囲んで指定します。 $\zeta$ の値を省略すると、最尤推定値が計算されます。SCALE=オプションは、ZETA=オプションの別名として指定できます。