UNIVARIATEプロシジャ
- 概要
-
入門ガイド

-
構文

-
詳細
 欠損値丸め記述統計量モードの計算パーセント点の計算位置の検定正規分布のパラメータに対する信頼限界ロバスト推定量ラインプリンタプロットの作成高解像度グラフの作成CLASSステートメントを使用した比較プロットの作成インセットの配置当てはめた連続分布の計算式適合度検定核密度推定Q-Qプロットと確率プロットの作成Q-Qプロットと確率プロットの解釈確率プロットとQ-Qプロットの分布Q-Qプロットを使用した形状パラメータの推定Q-Qプロットを使用した位置パラメータと尺度パラメータの推定Q-Qプロットを使用したパーセント点の推定入力データセットOUTPUTステートメントのOUT=出力データセットOUTHISTOGRAM=出力データセットOUTKERNEL=出力データセットOUTTABLE=出力データセット要約統計量のテーブルODSテーブル名当てはめた分布のODSテーブルODS Graphics計算リソース
欠損値丸め記述統計量モードの計算パーセント点の計算位置の検定正規分布のパラメータに対する信頼限界ロバスト推定量ラインプリンタプロットの作成高解像度グラフの作成CLASSステートメントを使用した比較プロットの作成インセットの配置当てはめた連続分布の計算式適合度検定核密度推定Q-Qプロットと確率プロットの作成Q-Qプロットと確率プロットの解釈確率プロットとQ-Qプロットの分布Q-Qプロットを使用した形状パラメータの推定Q-Qプロットを使用した位置パラメータと尺度パラメータの推定Q-Qプロットを使用したパーセント点の推定入力データセットOUTPUTステートメントのOUT=出力データセットOUTHISTOGRAM=出力データセットOUTKERNEL=出力データセットOUTTABLE=出力データセット要約統計量のテーブルODSテーブル名当てはめた分布のODSテーブルODS Graphics計算リソース -
例
 複数の変数に対する記述統計量の計算モードの計算極値オブザベーションと極値の表示度数表の作成基本要約プロットの作成FREQ変数を使用したデータセットの分析OUT=出力データセットへの要約統計量の保存出力データセットへのパーセント点の保存平均、標準偏差、分散に対する信頼限界の計算分位点とパーセント点に対する信頼限界の計算ロバスト推定の計算位置の検定ペアのデータを使用した符号検定の実行ヒストグラムの作成一元比較ヒストグラムの作成二元比較ヒストグラムの作成記述統計量を含むインセットの追加ヒストグラムのビン幅の指定正規曲線をヒストグラムに追加する当てはめた正規曲線を比較ヒストグラムに追加するベータ曲線の当てはめ対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ核密度推定の計算3パラメータ対数正規曲線の当てはめ折り重ねられた正規曲線の追加表示対数正規確率プロットの作成対数正規分布の当てはめを表示するヒストグラムの作成正規分位点プロットの作成分布参照線の追加正規分位点プロットの解釈対数正規分位点プロットから3パラメータを推定する対数正規分位点プロットからパーセント点を推定する対数正規分位点プロットからパラメータを推定するWeibull分布の分位点プロットの比較累積分布プロットの作成P-Pプロットの作成
複数の変数に対する記述統計量の計算モードの計算極値オブザベーションと極値の表示度数表の作成基本要約プロットの作成FREQ変数を使用したデータセットの分析OUT=出力データセットへの要約統計量の保存出力データセットへのパーセント点の保存平均、標準偏差、分散に対する信頼限界の計算分位点とパーセント点に対する信頼限界の計算ロバスト推定の計算位置の検定ペアのデータを使用した符号検定の実行ヒストグラムの作成一元比較ヒストグラムの作成二元比較ヒストグラムの作成記述統計量を含むインセットの追加ヒストグラムのビン幅の指定正規曲線をヒストグラムに追加する当てはめた正規曲線を比較ヒストグラムに追加するベータ曲線の当てはめ対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ核密度推定の計算3パラメータ対数正規曲線の当てはめ折り重ねられた正規曲線の追加表示対数正規確率プロットの作成対数正規分布の当てはめを表示するヒストグラムの作成正規分位点プロットの作成分布参照線の追加正規分位点プロットの解釈対数正規分位点プロットから3パラメータを推定する対数正規分位点プロットからパーセント点を推定する対数正規分位点プロットからパラメータを推定するWeibull分布の分位点プロットの比較累積分布プロットの作成P-Pプロットの作成 - リファレンス
次のセクションでは、HISTOGRAMステートメントで当てはめることができるパラメトリックな分布族の情報を示します。これらの分布の特性については、Johnson、KotzおよびBalakrishnan (1994、1995)により説明されています。
適合する密度関数は次のようになります。
ここで、![]() および
および
-
 下限しきい値パラメータ(下限端点パラメータ)
下限しきい値パラメータ(下限端点パラメータ)
-
 尺度パラメータ
尺度パラメータ
-
 形状パラメータ
形状パラメータ
-
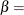 形状パラメータ
形状パラメータ
-
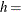 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
注: この表記は、HISTOGRAMステートメントを使って当てはめる他の分布の表記と一貫性があります。ただし、Johnson、KotzおよびBalakrishnan (1995)など多くのテキストで、ベータ密度関数は次のように記述されています。
これら2つのパラメータ化には次のような関係があります。
ベータ分布の範囲の下限はしきい値パラメータ![]() で、上限は
で、上限は![]() です。BETAオプションを使用して当てはめたベータ曲線を指定する場合、
です。BETAオプションを使用して当てはめたベータ曲線を指定する場合、![]() は最小データ値より小さく、
は最小データ値より小さく、![]() は最大データ値より大きい必要があります。
は最大データ値より大きい必要があります。![]() および
および![]() は、キーワードBETAの後のかっこ内のTHETA= / SIGMA= beta-optionsで指定できます。デフォルトでは、
は、キーワードBETAの後のかっこ内のTHETA= / SIGMA= beta-optionsで指定できます。デフォルトでは、![]() および
および![]() です。THETA=ESTおよびSIGMA=ESTを指定すると、
です。THETA=ESTおよびSIGMA=ESTを指定すると、![]() および
および![]() の最尤推定値が計算されます。ただし、3パラメータおよび4パラメータの最尤推定は、収束するとは限りません。
の最尤推定値が計算されます。ただし、3パラメータおよび4パラメータの最尤推定は、収束するとは限りません。
また、![]() および
および![]() は、それぞれALPHA=および BETA= beta-optionsで指定できます。デフォルトでは、
は、それぞれALPHA=および BETA= beta-optionsで指定できます。デフォルトでは、![]() および
および![]() の最尤推定値が計算されます。たとえば、下限が32、上限が212のデータセットに、
の最尤推定値が計算されます。たとえば、下限が32、上限が212のデータセットに、![]() および
および![]() の最尤推定値を使用するベータ密度曲線を当てはめるには、次のステートメントを使用します。
の最尤推定値を使用するベータ密度曲線を当てはめるには、次のステートメントを使用します。
histogram Length / beta(theta=32 sigma=180);
ベータ分布は、Pearson Type IまたはType II分布とも呼ばれます。これには、べき関数分布(![]() )、逆正弦分布(
)、逆正弦分布(![]() )、一般化逆正弦分布(
)、一般化逆正弦分布(![]() 、
、![]() )などが含まれます。
)などが含まれます。
ベータ分布の分位点はDATAステップ関数QUANTILEを使用して、ベータ分布の確率はDATAステップ関数CDFを使用して計算できます。
適合する密度関数は次のようになります。
ここで、
-
 しきい値パラメータ
しきい値パラメータ
-
 尺度パラメータ
尺度パラメータ 
-
 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
しきい値パラメータ![]() は、最小データ値以下である必要があります。
は、最小データ値以下である必要があります。![]() は、THRESHOLD= exponential-optionで指定できます。デフォルトは、
は、THRESHOLD= exponential-optionで指定できます。デフォルトは、![]() です。THETA=ESTを指定すると、
です。THETA=ESTを指定すると、![]() の最尤推定値が計算されます。また、
の最尤推定値が計算されます。また、![]() はSCALE= exponential-optionを使用して指定できます。デフォルトでは、
はSCALE= exponential-optionを使用して指定できます。デフォルトでは、![]() の最尤推定値が計算されます。著者によっては、尺度パラメータを
の最尤推定値が計算されます。著者によっては、尺度パラメータを![]() と定義している場合があります。
と定義している場合があります。
指数分布は、特殊なケースのガンマ分布(![]() の場合)およびWeibull分布(
の場合)およびWeibull分布(![]() の場合)です。関連分布は極値分布です。
の場合)です。関連分布は極値分布です。![]() が指数分布である場合、Xは極値分布です。
が指数分布である場合、Xは極値分布です。
指数分布の分位点はDATAステップ関数QUANTILEを使用して、指数分布の確率はDATAステップ関数CDFを使用して計算できます。
適合する密度関数は次のようになります。
ここで、
-
 しきい値パラメータ
しきい値パラメータ
-
 尺度パラメータ
尺度パラメータ
-
 形状パラメータ
形状パラメータ
-
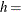 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
しきい値パラメータ![]() は、最小データ値未満である必要があります。
は、最小データ値未満である必要があります。![]() は、THRESHOLD= gamma-optionで指定できます。デフォルトは、
は、THRESHOLD= gamma-optionで指定できます。デフォルトは、![]() です。THETA=ESTを指定すると、
です。THETA=ESTを指定すると、![]() の最尤推定値が計算されます。また、
の最尤推定値が計算されます。また、![]() および
および![]() は、それぞれSCALE=およびALPHA= gamma-optionsで指定できます。デフォルトでは、
は、それぞれSCALE=およびALPHA= gamma-optionsで指定できます。デフォルトでは、![]() および
および![]() の最尤推定値が計算されます。
の最尤推定値が計算されます。
ガンマ分布はPearson Type III分布とも呼ばれ、カイ2乗、指数およびErlangの各分布が含まれます。カイ2乗分布の確率密度関数は次のとおりです。
これは、![]() 、
、![]() 、
、![]() のガンマ分布であることに注意してください。指数分布は
のガンマ分布であることに注意してください。指数分布は![]() のガンマ分布であり、Erlang分布は
のガンマ分布であり、Erlang分布は![]() が正の整数のガンマ分布です。関連分布はレイリー分布です。
が正の整数のガンマ分布です。関連分布はレイリー分布です。![]() の場合(ここで
の場合(ここで![]() は独立した
は独立した![]() 変数)、
変数)、![]() は次の確率密度関数に従う
は次の確率密度関数に従う![]() 分布になります。
分布になります。
![]() の場合、前述の分布はレイリー分布と呼ばれます。
の場合、前述の分布はレイリー分布と呼ばれます。
ガンマ分布の分位点はDATAステップ関数QUANTILEを使用して、ガンマ分布の確率はDATAステップ関数CDFを使用して計算できます。
適合する密度関数は次のようになります。
ここで、
-
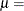 位置パラメータ
位置パラメータ
-
 尺度パラメータ
尺度パラメータ
-
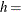 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
![]() および
および![]() は、それぞれMU=およびSIGMA= Gumbel-optionsで指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
は、それぞれMU=およびSIGMA= Gumbel-optionsで指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
注: Gumbel分布はType 1極値分布とも呼ばれます。
注: 乱数変数XがGumbel (Type 1極値)分布になるのは、![]() がWeibull分布で
がWeibull分布で![]() が標準指数分布である場合のみです。
が標準指数分布である場合のみです。
適合する密度関数は次のようになります。
ここで、
-
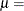 位置パラメータ
位置パラメータ
-
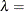 形状パラメータ
形状パラメータ
-
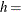 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
位置パラメータ![]() は、0より大きい必要があります。
は、0より大きい必要があります。![]() は、MU= iGauss-optionで指定できます。また、形状パラメータ
は、MU= iGauss-optionで指定できます。また、形状パラメータ![]() は、LAMBDA= iGauss-optionで指定できます。デフォルトでは、
は、LAMBDA= iGauss-optionで指定できます。デフォルトでは、![]() および
および![]() の最尤推定値が計算されます。
の最尤推定値が計算されます。
注: 特殊なケース(![]() および
および![]() の場合)では、Wald分布に一致します。
の場合)では、Wald分布に一致します。
逆ガウス分布の分位点はDATAステップ関数QUANTILEを使用して、逆ガウス分布の確率はDATAステップ関数CDFを使用して計算できます。
適合する密度関数は次のようになります。
ここで、
-
 しきい値パラメータ
しきい値パラメータ
-
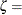 尺度パラメータ
尺度パラメータ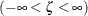
-
 形状パラメータ
形状パラメータ
-
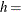 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
しきい値パラメータ![]() は、最小データ値未満である必要があります。
は、最小データ値未満である必要があります。![]() は、THRESHOLD= lognormal-optionで指定できます。デフォルトは、
は、THRESHOLD= lognormal-optionで指定できます。デフォルトは、![]() です。THETA=ESTを指定すると、
です。THETA=ESTを指定すると、![]() の最尤推定値が計算されます。
の最尤推定値が計算されます。![]() および
および![]() は、それぞれSCALE=およびSHAPE= lognormal-optionsで指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
は、それぞれSCALE=およびSHAPE= lognormal-optionsで指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
注: 対数正規分布は、Johnson系分布では![]() 分布とも呼ばれます。
分布とも呼ばれます。
Note: このマニュアルでは、対数正規分布の形状パラメータを![]() で表記していますが、他の分布の尺度パラメータの表記でも
で表記していますが、他の分布の尺度パラメータの表記でも![]() を使用しています。対数正規分布の形状パラメータの表記に
を使用しています。対数正規分布の形状パラメータの表記に![]() を使用するのは、Xが対数正規分布である場合に、
を使用するのは、Xが対数正規分布である場合に、![]() が標準正規分布になることに基づいています。この関係に基づき、対数正規分布の分位点はDATAステップ関数PROBIT、確率はDATAステップ関数PROBNORMを使用して計算できます。
が標準正規分布になることに基づいています。この関係に基づき、対数正規分布の分位点はDATAステップ関数PROBIT、確率はDATAステップ関数PROBNORMを使用して計算できます。
適合する密度関数は次のようになります。
ここで、
-
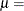 平均
平均
-
 標準偏差
標準偏差
-
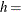 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
![]() および
および![]() はそれぞれMU=およびSIGMA= normal-optionsで指定できます。デフォルトでは、
はそれぞれMU=およびSIGMA= normal-optionsで指定できます。デフォルトでは、![]() を標本平均で、
を標本平均で、![]() を標本標準偏差で推定します。
を標本標準偏差で推定します。
正規分布の分位点はDATAステップ関数QUANTILEを使用して、正規分布の確率はDATAステップ関数CDFを使用して計算できます。
注: 正規分布は、Johnson系分布では![]() 分布とも呼ばれます。
分布とも呼ばれます。
適合する密度関数は次のようになります。
ここで、
-
 しきい値パラメータ
しきい値パラメータ
-
 形状パラメータ
形状パラメータ
-
 形状パラメータ
形状パラメータ
-
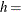 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
分布のサポートは、![]() (
(![]() の場合)および
の場合)および![]() (
(![]() の場合)です。
の場合)です。
注: 特殊なケースのパレート分布(![]() および
および![]() の場合)は、平均
の場合)は、平均![]() の指数分布および間隔
の指数分布および間隔![]() の一様分布にそれぞれ対応します。
の一様分布にそれぞれ対応します。
しきい値パラメータ![]() は、最小データ値未満である必要があります。
は、最小データ値未満である必要があります。![]() は、THETA= Pareto-optionで指定できます。デフォルトは
は、THETA= Pareto-optionで指定できます。デフォルトは![]() です。
です。![]() および
および![]() は、それぞれALPHA=およびSIGMA= Pareto-optionsでも指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
は、それぞれALPHA=およびSIGMA= Pareto-optionsでも指定できます。デフォルトでは、これらのパラメータの最尤推定値が計算されます。
注: パラメータの最尤推定量は![]() の場合は有効ですが、それ以外の場合は有効ではありません。この場合、推定量は漸近的に正規分布に従い、漸近的に有効になります。漸近正規分布に従う最尤推定値では、平均は
の場合は有効ですが、それ以外の場合は有効ではありません。この場合、推定量は漸近的に正規分布に従い、漸近的に有効になります。漸近正規分布に従う最尤推定値では、平均は![]() となり、分散共分散行列は次のようになります。
となり、分散共分散行列は次のようになります。
注:次の空間で極小がない場合、
最尤推定量は存在しません。最尤推定量の算出方法および推奨アルゴリズムの詳細は、Grimshaw(1993)で説明されています。
適合する密度関数は次のようになります。
ここで、
-
 下限しきい値パラメータ(下限端点パラメータ)
下限しきい値パラメータ(下限端点パラメータ)
-
 尺度パラメータ
尺度パラメータ
-
 形状パラメータ
形状パラメータ
-
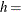 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
注: この表記は、HISTOGRAMステートメントを使って当てはめる他の分布の表記と一貫性があります。ただし、Johnson、KotzおよびBalakrishnan (1995)など多くのテキストで、べき関数分布の密度関数は次のように記述されています。
これら2つのパラメータ化には次のような関係があります。
注:べき関数分布族は、次の密度関数のベータ分布の部分集合です。
ここで、![]() であり、パラメータ
であり、パラメータ![]() です。したがって、ベータ分布の特性および推定手順がすべて適用されます。
です。したがって、ベータ分布の特性および推定手順がすべて適用されます。
べき関数分布の範囲の下限はしきい値パラメータ![]() で、上限は
で、上限は![]() です。POWERオプションを使用して当てはめたべき関数曲線を指定する場合、
です。POWERオプションを使用して当てはめたべき関数曲線を指定する場合、![]() は最小データ値より小さく、
は最小データ値より小さく、![]() は最大データ値より大きい必要があります。
は最大データ値より大きい必要があります。![]() および
および![]() は、キーワードPOWERの後のかっこ内のTHETA= / SIGMA= power-optionsで指定できます。デフォルトでは、
は、キーワードPOWERの後のかっこ内のTHETA= / SIGMA= power-optionsで指定できます。デフォルトでは、![]() および
および![]() です。THETA=ESTおよびSIGMA=ESTを指定すると、
です。THETA=ESTおよびSIGMA=ESTを指定すると、![]() および
および![]() の最尤推定値が計算されます。ただし、3パラメータの最尤推定は、収束するとは限りません。
の最尤推定値が計算されます。ただし、3パラメータの最尤推定は、収束するとは限りません。
また、![]() はALPHA= power-optionを使用して指定できます。デフォルトでは、
はALPHA= power-optionを使用して指定できます。デフォルトでは、![]() の最尤推定値が計算されます。たとえば、下限が32、上限が212のデータに、
の最尤推定値が計算されます。たとえば、下限が32、上限が212のデータに、![]() の最尤推定値を使用するべき関数密度曲線を当てはめるには、次のステートメントを使用します。
の最尤推定値を使用するべき関数密度曲線を当てはめるには、次のステートメントを使用します。
histogram Length / power(theta=32 sigma=180);
適合する密度関数は次のようになります。
ここで、
-
 下限しきい値パラメータ(下限端点パラメータ)
下限しきい値パラメータ(下限端点パラメータ)
-
 尺度パラメータ
尺度パラメータ
-
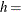 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
注:レイリー分布は、次の密度関数のWeibull分布です。
形状パラメータは![]() で、尺度パラメータは
で、尺度パラメータは![]() です。
です。
しきい値パラメータ![]() は、最小データ値未満である必要があります。
は、最小データ値未満である必要があります。![]() は、THETA= Rayleigh-optionで指定できます。デフォルトは
は、THETA= Rayleigh-optionで指定できます。デフォルトは![]() です。また、
です。また、![]() は、SIGMA= Rayleigh-optionでも指定できます。デフォルトでは、
は、SIGMA= Rayleigh-optionでも指定できます。デフォルトでは、![]() の最尤推定値が計算されます。
の最尤推定値が計算されます。
たとえば、下限が32のデータセットに![]() の最尤推定値を使用するレイリー密度曲線を当てはめるには、次のステートメントを使用します。
の最尤推定値を使用するレイリー密度曲線を当てはめるには、次のステートメントを使用します。
histogram Length / rayleigh(theta=32);
適合する密度関数は次のようになります。
![\[ p(x) = \left\{ \begin{array}{ll} \frac{\delta hv}{\sigma \sqrt {2\pi } } \left[ \left( \frac{x - \theta }{\sigma } \right) \left( 1 - \frac{x - \theta }{\sigma } \right) \right]^{-1} \times & \\ \exp \left[ -\frac{1}{2} \left( \gamma + \delta \log ( \frac{x - \theta }{\theta + \sigma -x} ) \right)^2 \right] & \mbox{for } \theta < x < \theta + \sigma \\ 0 & \mbox{for } x \leq \theta \text { or } x \geq \theta + \sigma \end{array} \right. \]](images/procstat_univariate0342.png)
ここで、
-
 しきい値パラメータ
しきい値パラメータ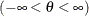
-
 尺度パラメータ
尺度パラメータ
-
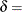 形状パラメータ
形状パラメータ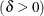
-
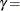 形状パラメータ
形状パラメータ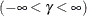
-
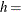 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
![]() 分布の下限はパラメータ
分布の下限はパラメータ![]() で、上限は値
で、上限は値![]() です。パラメータ
です。パラメータ![]() は最小データ値未満である必要があります。
は最小データ値未満である必要があります。![]() は、THETA=
は、THETA= ![]() -optionで指定できます。または、THETA = ESTの
-optionで指定できます。または、THETA = ESTの![]() -optionを使用すると、
-optionを使用すると、![]() の推定を要求できます。
の推定を要求できます。![]() のデフォルト値は0です。合計
のデフォルト値は0です。合計![]() は最小データ値よりも大きくなければなりません。
は最小データ値よりも大きくなければなりません。![]() のデフォルト値は0です。
のデフォルト値は0です。![]() は、SIGMA=
は、SIGMA= ![]() -optionで指定できます。または、SIGMA = ESTの
-optionで指定できます。または、SIGMA = ESTの![]() -optionを使用すると、
-optionを使用すると、![]() の推定を要求できます。
の推定を要求できます。
デフォルトでは、Slifker and Shapiro (1980)が示したパーセント点の方式を使用して、パラメータが推定されます。この方式は、![]() 、
、![]() 、
、![]() 、
、![]() で表される4つのデータパーセント点に基づいており、変換時に
で表される4つのデータパーセント点に基づいており、変換時に![]() 、
、![]() 、z、
、z、![]() で表される、標準正規分布の4つの均等間隔のパーセント点にそれらが対応しています。
で表される、標準正規分布の4つの均等間隔のパーセント点にそれらが対応しています。
zのデフォルト値は0.524です。当てはめの結果はzの選択に依存するため、FITINTERVAL=オプションを使用して他の値を(SBオプションの後にかっこで囲んで)指定できます。パーセント点法を使用する場合には、アプリケーションにとって重要なパーセント点に対応するzの値を選択することが必要です。
次の値は、データパーセント値から計算されます。
これはSlifker and Shapiro (1980)により証明されました。
![\[ \begin{array}{ll} \frac{mn}{p^2} > 1 & \mbox{for any }S_ U\text { distribution} \\ \frac{mn}{p^2} < 1 & \mbox{for any }S_ B\text { distribution} \\ \frac{mn}{p^2} = 1 & \mbox{for any }S_ L\text { (lognormal) distribution} \\ \end{array} \]](images/procstat_univariate0357.png)
プラスマイナス1の許容誤差区分を使用することにより、この比条件で3つのファミリ間を区別します。許容誤差は、FITTOLERANCE=オプションで指定できます(SBオプションの後にかっこで囲んで指定します)。デフォルトの許容誤差は0.01です。 この基準は、次の不等式を満たすとします。
![]() 分布のパラメータを計算するには、Slifker and Shapiro (1980)により導出された明示的な公式を使用します。
分布のパラメータを計算するには、Slifker and Shapiro (1980)により導出された明示的な公式を使用します。
FITMETHOD = MOMENTSを(SBオプションの後にかっこで囲んで)指定すると、積率法がパラメータ推定に使用されます。 FITMETHOD = MLEを(SBオプションの後にかっこで囲んで)指定すると、最尤法がパラメータ推定に使用されます。ただし、最尤推定値は必ず存在するとは限りません。Johnson分布を当てはめる方法については、Bowman and Shenton (1983)を参照してください。
適合する密度関数は次のようになります。
![\[ p(x) = \left\{ \begin{array}{ll} \frac{ \delta hv}{\sigma \sqrt {2\pi } } \frac{ 1 }{ \sqrt { 1 + \left( (x - \theta ) / \sigma \right)^2 } } \times & \\ \exp \left[ -\frac{1}{2} \left( \gamma + \delta \sinh ^{-1} \left( \frac{x - \theta }{\sigma } \right) \right)^2 \right] & \mbox{for } x > \theta \\ 0 & \mbox{for } x \leq \theta \end{array} \right. \]](images/procstat_univariate0359.png)
ここで、
-
 位置パラメータ
位置パラメータ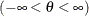
-
 尺度パラメータ
尺度パラメータ
-
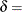 形状パラメータ
形状パラメータ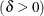
-
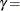 形状パラメータ
形状パラメータ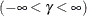
-
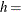 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
パラメータは、THETA= / SIGMA= / DELTA= / GAMMA= ![]() -optionsで指定できます。これらのオプションはSUオプションの後にかっこで囲んで指定します。これらのパラメータを指定しなかった場合は、それぞれ推定されます。
-optionsで指定できます。これらのオプションはSUオプションの後にかっこで囲んで指定します。これらのパラメータを指定しなかった場合は、それぞれ推定されます。
デフォルトでは、Slifker and Shapiro (1980)が示したパーセント点の方式を使用して、パラメータが推定されます。この方式は、![]() 、
、![]() 、
、![]() 、
、![]() で表される4つのデータパーセント点に基づいており、変換時に
で表される4つのデータパーセント点に基づいており、変換時に![]() 、
、![]() 、z、
、z、![]() で表される、標準正規分布の4つの均等間隔のパーセント点にそれらが対応しています。
で表される、標準正規分布の4つの均等間隔のパーセント点にそれらが対応しています。
zのデフォルト値は0.524です。当てはめの結果はzの選択に依存するため、FITINTERVAL=オプションを使用して他の値を(SUオプションの後にかっこで囲んで)指定できます。パーセント点法を使用する場合には、アプリケーションにとって重要なパーセント点に対応するzの値を選択することが必要です。
次の値は、データパーセント値から計算されます。
これはSlifker and Shapiro (1980)により証明されました。
![\[ \begin{array}{ll} \frac{mn}{p^2} > 1 & \mbox{for any }S_ U\text { distribution} \\ \frac{mn}{p^2} < 1 & \mbox{for any }S_ B\text { distribution} \\ \frac{mn}{p^2} = 1 & \mbox{for any }S_ L\text { (lognormal) distribution} \\ \end{array} \]](images/procstat_univariate0357.png)
プラスマイナス1の許容誤差区分を使用することにより、この比条件で3つのファミリ間を区別します。許容誤差は、FITTOLERANCE=オプションで指定できます(SUオプションの後にかっこで囲んで指定します)。デフォルトの許容誤差は0.01です。 この基準は、次の不等式を満たすとします。
![]() 分布のパラメータを計算するには、Slifker and Shapiro (1980)により導出された明示的な公式を使用します。
分布のパラメータを計算するには、Slifker and Shapiro (1980)により導出された明示的な公式を使用します。
FITMETHOD = MOMENTSを(SUオプションの後にかっこで囲んで)指定すると、積率法がパラメータ推定に使用されます。 FITMETHOD = MLEを(SUオプションの後にかっこで囲んで)指定すると、最尤法がパラメータ推定に使用されます。ただし、最尤推定値は必ず存在するとは限りません。Johnson分布を当てはめる方法については、Bowman and Shenton (1983)を参照してください。
適合する密度関数は次のようになります。
ここで、
-
 しきい値パラメータ
しきい値パラメータ
-
 尺度パラメータ
尺度パラメータ
-
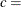 形状パラメータ
形状パラメータ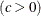
-
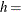 ヒストグラム間隔の幅
ヒストグラム間隔の幅
-
 垂直比率
垂直比率
および
![\[ v = \left\{ \begin{array}{ll} n & \mbox{the sample size, for VSCALE=COUNT} \\ 100 & \mbox{for VSCALE=PERCENT} \\ 1 & \mbox{for VSCALE=PROPORTION} \end{array} \right. \]](images/procstat_univariate0285.png)
しきい値パラメータ![]() は、最小データ値未満である必要があります。
は、最小データ値未満である必要があります。![]() は、THRESHOLD= Weibull-optionで指定できます。デフォルトは、
は、THRESHOLD= Weibull-optionで指定できます。デフォルトは、![]() です。THETA=ESTを指定すると、
です。THETA=ESTを指定すると、![]() の最尤推定値が計算されます。
の最尤推定値が計算されます。![]() およびcは、それぞれ、SCALE=およびSHAPE= Weibull-optionsで指定できます。デフォルトでは、
およびcは、それぞれ、SCALE=およびSHAPE= Weibull-optionsで指定できます。デフォルトでは、![]() およびcの最尤推定値をプロシジャが計算します。
およびcの最尤推定値をプロシジャが計算します。
指数分布は、特殊なケースのWeibull分布(![]() の場合)です。
の場合)です。
Weibull分布の分位点はDATAステップ関数QUANTILEを使用して、Weibull分布の確率はDATAステップ関数CDFを使用して計算できます。