UNIVARIATEプロシジャ

例4.25 折り重ねられた正規曲線の追加表示

この例は、HISTOGRAMステートメントでサポートされていない当てはめた曲線の表示方法を示しています。多くの製造済み組み立て品の取り付け位置のオフセット(mm)が測定され、測定値(Offset)はAssemblyという名前のデータセットに保存されます。次のステートメントはデータセットAssemblyを作成します。 

data Assembly;
   label Offset = 'Offset (in mm)';
   input Offset @@;
   datalines;
11.11 13.07 11.42  3.92 11.08  5.40 11.22 14.69  6.27  9.76
 9.18  5.07  3.51 16.65 14.10  9.69 16.61  5.67  2.89  8.13
 9.97  3.28 13.03 13.78  3.13  9.53  4.58  7.94 13.51 11.43
11.98  3.90  7.67  4.32 12.69  6.17 11.48  2.82 20.42  1.01
 3.18  6.02  6.63  1.72  2.42 11.32 16.49  1.22  9.13  3.34
 1.29  1.70  0.65  2.62  2.04 11.08 18.85 11.94  8.34  2.07
 0.31  8.91 13.62 14.94  4.83 16.84  7.09  3.37  0.49 15.19
 5.16  4.14  1.92 12.70  1.97  2.10  9.38  3.18  4.18  7.22
15.84 10.85  2.35  1.93  9.19  1.39 11.40 12.20 16.07  9.23
 0.05  2.15  1.95  4.39  0.48 10.16  4.81  8.28  5.68 22.81
 0.23  0.38 12.71  0.06 10.11 18.38  5.53  9.36  9.32  3.63
12.93 10.39  2.05 15.49  8.12  9.52  7.77 10.70  6.37  1.91
 8.60 22.22  1.74  5.84 12.90 13.06  5.08  2.09  6.41  1.40
15.60  2.36  3.97  6.17  0.62  8.56  9.36 10.19  7.16  2.37
12.91  0.95  0.89  3.82  7.86  5.33 12.92  2.64  7.92 14.06
;

折り重ねられた正規分布をオフセットの測定に当てはめることが決定されます。変数Xは、$X=|Y|$の場合に折り重ねられた正規分布になり、ここで、Yは$N(\mu ,\sigma )$のような分布です。当てはめた密度は次のとおりです。

\[ h(x) = \frac{1}{\sqrt {2\pi } \sigma } \left[ \exp \left( -\frac{(x-\mu )^2}{2\sigma ^2} \right) + \exp \left( -\frac{(x+\mu )^2}{2\sigma ^2} \right) \right] \]

ここで、$x \geq 0$です。

SAS/IMLを使用して、Elandt (1961)が定義した積率法に基づく$\mu $および$\sigma $の予備的な推定値を計算できます。これらの推定値はElandt (1961)の(19)を解くことによって計算されます。この式は次のように定義されます。

\[ f(\theta ) = \frac{\left( \frac{2}{\sqrt {2\pi }} e^{-\theta ^2/2 } - \theta \left[ 1-2\Phi (\theta ) \right] \right)^2}{1+\theta ^2} = A \]

ここで、$\Phi (\cdot )$は標準正規分布関数であり、次の式が成り立ちます。

\[ A = \frac{ \bar{x}^2 }{ \frac{1}{n} \sum _{i=1}^ n x_ i^2 } \]

この場合、$\sigma $および$\mu $の推定値は次のように求められます。

\[ \begin{array}{lll} \hat{\sigma }_0 & = \sqrt { \frac{ \frac{1}{n} \sum _{i=1}^ n x_ i^2}{1 + \hat{\theta }^2 } } \\ \hat{mu}_0 & = \hat{\theta } \cdot \hat{\sigma }_0 \end{array} \]

まず、MEANSプロシジャによる1番目および2番目の積率の計算と、次のDATAステップによる定数 Aの計算を行います。 

proc means data = Assembly noprint;
   var Offset;
   output out=stat mean=m1 var=var n=n min = min;
run;

* Compute constant A from equation (19) of Elandt (1961);
data stat;
   keep m2 a min;
   set stat;
   a  = (m1*m1);
   m2 = ((n-1)/n)*var + a;
   a  = a/m2;
run;

次に、SAS/IMLサブルーチンNLPDDを使用して、$(f(\theta )-A)^2$を最小化することにより式(19)を解き、$\hat{mu}_0$および$\hat{\sigma }_0$を計算します。 

proc iml;
   use stat;
   read all var {m2}  into m2;
   read all var {a}   into a;
   read all var {min} into min;

   * f(t) is the function in equation (19) of Elandt (1961);
   start f(t) global(a);
     y = .39894*exp(-0.5*t*t);
     y = (2*y-(t*(1-2*probnorm(t))))**2/(1+t*t);
     y = (y-a)**2;
     return(y);
   finish;

   * Minimize (f(t)-A)**2 and estimate mu and sigma;
   if ( min < 0 ) then do;
      print "Warning: Observations are not all nonnegative.";
      print "     The folded normal is inappropriate.";
      stop;
      end;
   if ( a < 0.637 ) then do;
      print "Warning: the folded normal may be inappropriate";
      end;
   opt = { 0 0 };
   con = { 1e-6 };
   x0  = { 2.0 };
   tc  = { . . . . . 1e-8 . . . . . . .};
   call nlpdd(rc,etheta0,"f",x0,opt,con,tc);
   esig0 = sqrt(m2/(1+etheta0*etheta0));
   emu0  = etheta0*esig0;

   create prelim var {emu0 esig0 etheta0};
   append;
   close prelim;

   * Define the log likelihood of the folded normal;
   start g(p) global(x);
      y = 0.0;
      do i = 1 to nrow(x);
         z = exp( (-0.5/p[2])*(x[i]-p[1])*(x[i]-p[1]) );
         z = z + exp( (-0.5/p[2])*(x[i]+p[1])*(x[i]+p[1]) );
         y = y + log(z);
      end;
      y = y - nrow(x)*log( sqrt( p[2] ) );
      return(y);
   finish;
   * Maximize the log likelihood with subroutine NLPDD;
   use assembly;
   read all var {offset} into x;
   esig0sq = esig0*esig0;
   x0      = emu0||esig0sq;
   opt     = { 1 0 };
   con     = { . 0.0, .  .  };
   call nlpdd(rc,xr,"g",x0,opt,con);
   emu     = xr[1];
   esig    = sqrt(xr[2]);
   etheta  = emu/esig;
   create parmest var{emu esig etheta};
   append;
   close parmest;
quit;

出力4.25.1に示されているように、予備的な推定値がデータセットPrelimに保存されます。

出力4.25.1: $\mu $、$\sigma $、$\theta $の予備的な推定値

データセットPrelim

Obs EMU0 ESIG0 ETHETA0
1 6.51735 6.54953 0.99509 




            

            


            
ここで、$\hat{mu}_0$および$\hat{\sigma }_0$を初期推定値として使用して、NLPDDサブルーチンを呼び出し、折り重ねられた正規分布の対数尤度$l(\mu ,\sigma )$を(ここでは定数になるまで)最大化します。
            

            

               
\[  l(\mu ,\sigma ) = -n \log \sigma + \sum _{i=1}^ n \log \left[ \exp \left( -\frac{(x_ i-\mu )^2}{2\sigma ^2} \right) + \exp \left( -\frac{(x_ i+\mu )^2}{2\sigma ^2} \right) \right]  \]

            


* Define the log likelihood of the folded normal;
start g(p) global(x);
   y = 0.0;
   do i = 1 to nrow(x);
      z = exp( (-0.5/p[2])*(x[i]-p[1])*(x[i]-p[1]) );
      z = z + exp( (-0.5/p[2])*(x[i]+p[1])*(x[i]+p[1]) );
      y = y + log(z);
   end;
   y = y - nrow(x)*log( sqrt( p[2] ) );
   return(y);
finish;
* Maximize the log likelihood with subroutine NLPDD;
use assembly;
read all var {offset} into x;
esig0sq = esig0*esig0;
x0      = emu0||esig0sq;
opt     = { 1 0 };
con     = { . 0.0, .  .  };
call nlpdd(rc,xr,"g",x0,opt,con);
emu     = xr[1];
esig    = sqrt(xr[2]);
etheta  = emu/esig;
create parmest var{emu esig etheta};
append;
close parmest;
quit;



出力4.25.2に示されているように、データセットParmEstには、 最尤推定値$\hat{mu}$と$\hat{\sigma }$ (および$\hat{mu}/\hat{\sigma }$)が含められます。
            

            
  

            


出力4.25.2: $\mu $、$\sigma $、$\theta $の最終推定値

               

                  

                     
                     

                        
                        
                        

データセットParmEst
                              
                           



                           
                           

                              
                              









Obs
                                       
                                       EMU
                                       
                                       ESIG
                                       
                                       ETHETA
                                       
                                    



1
                                       
                                       6.66761
                                       
                                       6.39650
                                       
                                       1.04239
                                       
                                    





                           
                        

                        



                     
                     
                  





            

            


            
曲線をヒストグラムに追加するため、まずヒストグラム間隔の幅と端点を計算します。次のステートメントは、これらの値をOutCalcというデータセットに保存します。なお、プロットはこの時点では作成されません。
            


proc univariate data = Assembly noprint;
   histogram Offset / outhistogram = out normal(noprint) noplot;
run;

data OutCalc (drop = _MIDPT_);
   set out (keep = _MIDPT_) end = eof;
   retain _MIDPT1_ _WIDTH_;
   if _N_ = 1 then _MIDPT1_ = _MIDPT_;
   if eof then do;
      _MIDPTN_ = _MIDPT_;
      _WIDTH_ = (_MIDPTN_ - _MIDPT1_) / (_N_ - 1);
      output;
   end;
run;



出力4.25.3はデータセットOutCalcのリストを示しています。ヒストグラムのバーの幅は、変数_WIDTH_の値として保存されます。最初と最後のヒストグラムのバーの中間点は、変数_MIDPT1_および_MIDPTN_の値として保存されます。
            

            
  

            


出力4.25.3: データセットOutCalc

               

                  

                     
                     

                        
                        
                        

データセットOutCalc
                              
                           



                           
                           

                              
                              









Obs
                                       
                                       _MIDPT1_
                                       
                                       _WIDTH_
                                       
                                       _MIDPTN_
                                       
                                    



1
                                       
                                       1.5
                                       
                                       3
                                       
                                       22.5
                                       
                                    





                           
                        

                        



                     
                     
                  





            

            


            
次のステートメントはAnnoという名前の注釈データセットを作成し、そのデータセットに当てはめた曲線の座標を格納します。
            


data Anno;
   merge ParmEst OutCalc;
   length function color $ 8;
   function = 'point';
   color    = 'black';
   size     =  2;
   xsys     = '2';
   ysys     = '2';
   when     = 'a';
   constant = 39.894*_width_;;
   left     =  _midpt1_ - .5*_width_;
   right    =  _midptn_ + .5*_width_;
   inc      = (right-left)/100;
   do x = left to right by inc;
      z1 = (x-emu)/esig;
      z2 = (x+emu)/esig;
      y  = (constant/esig)*(exp(-0.5*z1*z1)+exp(-0.5*z2*z2));
      output;
      function = 'draw';
   end;
run;



次のステートメントはANNOTATE=データセットを読み込み、ヒストグラムと当てはめた曲線を表示します。


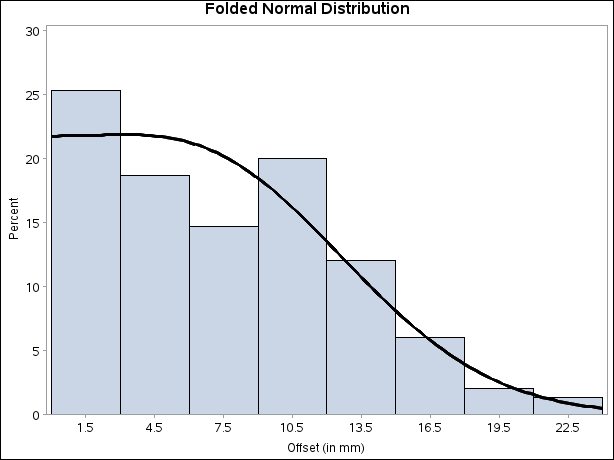
title 'Folded Normal Distribution';
ods graphics off;
proc univariate data=assembly noprint;
   histogram Offset / annotate = anno;
run;



出力4.25.4はヒストグラムと当てはめた曲線を表示しています。
            

            
  

            


出力4.25.4: 折り重ねられた正規曲線を追加表示したヒストグラム

               

                  
折り重ねられた正規曲線を追加表示したヒストグラム

               

            

            


            
この例のサンプルプログラムuniex15.sasは、Base SASソフトウェアのSASサンプルライブラリに含まれています。