UNIVARIATEプロシジャ

PROC UNIVARIATEステートメント

  • PROC UNIVARIATE <options>;

UNIVARIATEプロシジャを呼び出すには、PROC UNIVARIATEステートメントを使用する必要があります。PROC UNIVARIATEステートメント自体を使用してさまざまな統計量を要求し、各分析変数のデータ分布を要約することができます。

  • 標本積率

  • 位置とばらつきの基本統計量

  • 平均、標準偏差、分散に対する信頼区間

  • 位置の検定

  • 正規性の検定

  • トリム平均とウィンザー化平均

  • 尺度のロバスト推定

  • 分位点と関連信頼区間

  • 極値オブザベーションと極値

  • オブザベーションの度数

  • 欠損値

さらに、PROC UNIVARIATEステートメントのオプションを使用して、次のことができます。

  • 分析する入力データセットを指定

  • グラフカタログを指定して、従来的なグラフ出力を保存

  • 変数値の丸め単位を指定

  • パーセント点の計算に使用する定義を指定

  • 分散および標準偏差の計算に使用する分母を指定

  • ラインプリンタでプロットが作成されるように要求し、特徴に使用する特殊な印刷文字を定義

  • テーブルを抑制

  • 出力データセットの統計量を保存

PROC UNIVARIATEステートメントで使用できるオプションは次のとおりです。

ALL

FREQ 、MODES 、NEXTRVAL= 5、PLOTS 、CIBASIC オプションが生成するすべての統計量とテーブルを要求します。分析変数に重みが与えられていない場合、このオプションも、 CIPCTLDF 、 CIPCTLNORMAL 、LOCCOUNT 、NORMAL 、ROBUSTSCALE 、TRIMMED= .25、WINSORIZED= .25オプションが生成する統計量とテーブルを要求します。UNIVARIATEプロシジャは、また、ALPHA= 、MU0= 、NEXTRVAL=、CIBASIC、CIPCTLDF、CIPCTLNORMAL、TRIMMED=、WINSORIZED=のいずれかに指定した任意の値を使用して出力を生成します。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。

いくつかの信頼区間オプションで、特殊なALPHA=オプションが使用できます。たとえば、 CIBASIC (ALPHA=0.10)を指定して、90%水準の基本信頼限界のテーブルを要求できます。これらのオプションのデフォルト値は、PROCステートメントのALPHA=オプションの値です。

ANNOTATE=SAS-data-set
ANNO=SAS-data-set

SAS/GRAPH: Referenceで説明されているように、注釈変数を含む入力データセットを指定します。従来的なグラフに特徴を追加するには、このデータセットを使用します。プロシジャで作成されたすべてのグラフに対して、このデータセットの特徴が追加されます。プロットステートメントで従来的なグラフを作成しない場合、ANNOTATE=データセットは使用されません。このオプションは、ODS Graphics出力には適用されません。ステートメントで作成された特定のグラフに対して特徴を追加する場合は、プロットステートメントのANNOTATE=オプションを使用します。

CIBASIC <(<TYPE=keyword> <ALPHA=$\alpha $>)>

データが正規分布であることを前提にして、平均値、標準偏差および分散の信頼限界を要求します。CIBASICオプションを使用する場合は、VARDEF= のデフォルト値(DF)を使用する必要があります。

TYPE=keyword

信頼限界の種類を指定します。keywordには、LOWER、UPPER、TWOSIDEDのいずれかを指定できます。デフォルト値はTWOSIDEDです。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。デフォルト値は、PROCステートメントで指定された ALPHA= の値になります。

CIPCTLDF <(<TYPE=keyword> <ALPHA=$\alpha $>)>
CIQUANTDF <(<TYPE=keyword> <ALPHA=$\alpha $>)>

分布によらない手法に基づく分位点の信頼限界を要求します。つまり、正規分布などのパラメトリックな分布データを前提としません。UNIVARIATEプロシジャは、Hahn and Meeker (1991)の説明に基づき、順序統計量(順位)を使用して信頼限界を計算します。このオプションは、WEIGHT ステートメントを使用する場合には適用されません。

TYPE=keyword

信頼限界の種類を指定します。keywordには、LOWER、UPPER、SYMMETRIC、ASYMMETRICのいずれかを指定できます。デフォルト値はSYMMETRICです。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。デフォルト値は、PROCステートメントで指定された ALPHA= の値になります。

CIPCTLNORMAL <(<TYPE=keyword> <ALPHA=$\alpha $>)>
CIQUANTNORMAL <(<TYPE=keyword> <ALPHA=$\alpha $>)>

データが正規分布であることを前提にして、パーセント点の信頼限界を要求します。計算方法は、 Hahn and Meeker (1991)のセクション4.4.1で説明されており、Odeh and Owen (1980)によって示された非心t分布を使用します。このオプションは、WEIGHT ステートメントを使用する場合には適用されません。

TYPE=keyword

信頼限界の種類を指定します。keywordには、LOWER、UPPER、TWOSIDEDのいずれかを指定できます。デフォルト値はTWOSIDEDです。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。デフォルト値は、PROCステートメントで指定された ALPHA= の値になります。

DATA=SAS-data-set

分析する入力SASデータセットを指定します。DATA=オプションを省略すると、最後に作成されたSASデータセットが使用されます。

EXCLNPWGT
EXCLNPWGTS

重み値が非正数(0または負数)のオブザベーションを分析から除外します。デフォルトでは、重みが負または0のオブザベーションがオブザベーションの合計数にカウントされます。このオプションは、WEIGHT ステートメントを使用する場合のみ適用されます。

FREQ

変数値、度数、パーセンテージ、累積パーセンテージで構成される度数表を要求します。

WEIGHTステートメントを指定すると、UNIVARIATEプロシジャでは、重み付きの度数が度数表に含まれ、この値を使用してパーセンテージが計算されます。

GOUT=graphics-catalog

UNIVARIATEプロシジャが従来的なグラフ出力の保存に使用するSASカタログを指定します。graphics-catalogの名前のライブラリ参照名を省略すると、UNIVARIATEプロシジャでは、WORKと呼ばれる一時ライブラリからカタログが検索されます。存在しない場合はカタログが作成されます。 このオプションは、ODS Graphics出力には適用されません。

IDOUT

OUTPUTステートメントで作成される出力データセットに、ID変数を含めます。出力データセットのID変数の値は、入力データセットまたはBYグループの最初の値です。デフォルトでは、ID変数はOUTPUTステートメントのデータセットに含まれません。

LOCCOUNT

MU0=の値より大きい、等しくない、小さいオブザベーション数が表示されたテーブルを要求します。UNIVARIATEプロシジャでは、符号検定および符号付き順位検定にこれらの値を使用します。このオプションは、WEIGHT ステートメントを使用する場合には適用されません。

MODES|MODE

あらゆるモードのテーブルを要求します。デフォルトでは、データに複数のモードが含まれるときは、すべての基本統計量解析のうちで最も低水準のモードが表示されます。すべての値が重複しない場合は、モードのテーブルは作成されません。

MU0=values
LOCATION=values

"Tests for Location: Mu0=value"というラベルのテーブルに要約される位置検定の帰無仮説の平均値または位置パラメータ($\mu _0$)を指定します。1つの値を指定すると、すべての分析変数に対して同じ帰無仮説が検定されます。複数の値を指定すると、VARステートメントが要求され、2つのリストの順序で、分析変数、マッチング変数および位置の値ごとに異なる帰無仮説をUNIVARIATEプロシジャでは検定します。デフォルトのvalueは0です。

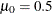次のステートメントは、最初の変数に対して仮定$\mu _0=0$を、2番目の変数に対して仮定$\mu _0=0.5$を検定します。 

proc univariate mu0=0 0.5;
NEXTROBS=n

極値オブザベーションテーブルに表示される極値オブザベーションの数を指定します。このテーブルには、最小値のオブザベーションがn個、最大値のオブザベーションがn個リストされます。デフォルト値は5です。NEXTROBS=0を指定すると、極値オブザベーションテーブルを抑制できます。

NEXTRVAL=n

極値テーブルに表示される極値の数を指定します。このテーブルには、重複のない最小値がn個、重複のない最大値がn個リストされます。デフォルトはn = 0で、テーブルは表示されません。

NOBYPLOT

BY ステートメントを使用した場合と、PROCステートメントでALL オプションまたはPLOTS オプションを使用した場合にデフォルトで作成される、ラインプリンタの横に並べた箱ひげ図を抑制します。

NOPRINT

PROC UNIVARIATEステートメントで作成される記述統計量のテーブルをすべて抑制します。NOPRINTを指定しても、HISTOGRAMステートメントで作成されるテーブルは抑制されません。HISTOGRAMステートメントのテーブルの作成を抑制するには、HISTOGRAMステートメントのNOPRINTオプションを使用します。OUT=またはOUTTABLE=出力データセットのみを作成する場合は、NOPRINTを使用します。

NORMAL
NORMALTEST

経験分布関数に基づいて、適合度検定などの正規性の検定を要求します。 Shapiro-Wilk検定(指定された標本サイズが2000以下)、Kolmogorov-Smirnov検定、Anderson-Darling検定、Cramér-von Mises検定の検定統計量とp値がテーブルに示されます。このオプションは、WEIGHT ステートメントを使用する場合には適用されません。

NOTABCONTENTS

PROC UNIVARIATEステートメントで作成される要約統計量テーブルの目次エントリのテーブルを抑制します。

NOVARCONTENTS

目次の分析変数に関連付けられたグループエントリを抑制します。デフォルトでは、目次には、変数名を持つグループの分析変数に関連付けられた結果が表示されます。

OUTTABLE=SAS-data-set

分析変数ごとに1つのオブザベーションの表形式にまとめられた、単変量統計量を含む出力データセットを作成します。詳細は、OUTTABLE=出力データセットのセクションを参照してください。

PCTLDEF=value
DEF=value

パーセント点を計算するときに使用される定義を指定します。デフォルト値は5です。値は1、2、3、4、5のいずれかです。重み付き分位点を計算する場合、PCTLDEF=は使用できません。分位点の定義の詳細は、パーセント点の計算のセクションを参照してください。

PLOTS | PLOT< ( <plot-options> <SSPLOT(plot-options)> ) >

分析変数ごとに複数のプロットから構成される1つのパネルを作成します。ODS Graphicsが有効である場合、このパネルには、水平ヒストグラム、箱ひげ図、正規確率プロットが含められます。それ以外の場合、ラインプリンタ出力を使用して、幹葉プロット(横棒グラフ)、箱ひげ図、正規確率プロットが作成されます。BYステートメントを指定すると、最後のBYグループの単変量出力に続いて、BYグループ内のデータの箱ひげ図が横に並べて表示されます。

ODS Graphicsが有効である場合、次のプロットオプションを指定することにより、プロットのタイトルやフットノートを作成できます。SSPLOTサブオプション内で指定したプロットオプションは、横に並べられたBYグループデータの箱ひげ図に適用されます。

ODSFOOTNOTE=FOOTNOTE | FOOTNOTE1 | 'string'

ODS Graphics出力にフットノートを追加します。FOOTNOTE (またはFOOTNOTE1)キーワードを指定すると、SAS FOOTNOTEステートメントを使用してグラフのフットノートが生成されます。引用符付きの文字列を指定すると、その文字列がフットノートとして使用されます。引用符付きの文字列には、次のようなエスケープ文字を含めることができます。これらは、分析に含まれている適切な値で置き換えられます。

$\backslash $n

分析変数名で置き換えられます。

$\backslash $l

分析変数のラベル(あるいは分析変数がラベルを持たない場合には分析変数名)で置き換えられます。

ODSFOOTNOTE2=FOOTNOTE2 | 'string'

ODS Graphics出力にセカンダリフットノートを追加します。FOOTNOTE2キーワードを指定すると、SAS FOOTNOTE2ステートメントを使用してグラフのセカンダリフットノートが生成されます。引用符付きの文字列を指定すると、その文字列がセカンダリフットノートとして使用されます。引用符付きの文字列には、次のようなエスケープ文字を含めることができます。これらは、分析に含まれている適切な値で置き換えられます。

$\backslash $n

分析変数名で置き換えられます。

$\backslash $l

分析変数のラベル(あるいは分析変数がラベルを持たない場合には分析変数名)で置き換えられます。

ODSTITLE=TITLE | TITLE1 | NONE | DEFAULT | LABELFMT | 'string'

ODS Graphics出力のタイトルを指定します。

TITLE (またはTITLE1)

SAS TITLEステートメントの値をグラフのタイトルとして使用します。

NONE

グラフのタイトルを一切表示しません。

デフォルト

デフォルトのODS Graphicsタイトル(プロットの種類と分析変数名から構成されるタイトル)を使用します。

LABELFMT

変数名の代わりに変数ラベルを含むデフォルトのODS Graphicsタイトルを使用します。

引用符付きの文字列を指定すると、その文字列がグラフのタイトルとして使用されます。引用符付きの文字列には、次のようなエスケープ文字を含めることができます。これらは、分析に含まれている適切な値で置き換えられます。

$\backslash $n

分析変数名で置き換えられます。

$\backslash $l

分析変数のラベル(あるいは分析変数がラベルを持たない場合には分析変数名)で置き換えられます。

ODSTITLE2=TITLE2 | 'string'

ODS Graphics出力のセカンダリタイトルを指定します。TITLE2キーワードを指定すると、SAS TITLE2ステートメントを使用してグラフのセカンダリタイトルが生成されます。引用符付きの文字列を指定すると、その文字列がグラフのセカンダリタイトルとして使用されます。引用符付きの文字列には、次のようなエスケープ文字を含めることができます。これらは、分析に含まれている適切な値で置き換えられます。

$\backslash $n

分析変数名で置き換えられます。

$\backslash $l

分析変数のラベル(あるいは分析変数がラベルを持たない場合には分析変数名)で置き換えられます。

注: ODSTITLE=LABELFMTオプションと、分析変数名や分析変数ラベルの置き換えは、SSPLOTサブオプション内で指定するプロットオプションではサポートされません。

PLOTSIZE=n

PLOTSオプションで要求したラインプリンタプロットに使用される大体の行数を指定します。nがSASシステムオプションのPAGESIZE=の値より大きい場合、UNIVARIATEプロシジャではPAGESIZE=の値が使用されます。nが8未満の場合は、8行でプロットされます。

ROBUSTSCALE

ロバスト(頑健)な尺度推定値でテーブルを作成します。統計量には、四分位範囲、Giniの平均差、中央絶対偏差(MAD)、RousseeuwとCroux (1993)が提唱した2つの統計量$Q_ n$および$S_ n$が含まれます。詳細は、尺度のロバスト推定のセクションを参照してください。このオプションは、WEIGHT ステートメントを使用する場合には適用されません。

ROUND=units

統計計算を実行する前に、分析変数を丸める単位を指定します。1つの単位を指定すると、その単位ですべての分析変数が丸められます。複数の単位を指定すると、VARステートメントが要求され、それぞれの単位により分析変数値が丸められます。ROUND=0の場合は、丸められません。 ROUND=オプションを指定すると、重複しない変数値の数が減少するため、プロシジャのメモリの消費量も減少します。たとえば、最初の分析変数の丸め単位を1にし、2番目の分析変数の丸め単位を0.5にするには、次のステートメントをサブミットします。 

proc univariate round=1 0.5;
   var Yieldstrength tenstren;
run;

変数値が、2つの最も近い丸められたポイントの中間にある場合、値は丸め値の最も近い偶数の倍数に丸められます。たとえば、丸め値が1の場合、変数値-2.5、-2.2および-1.5は-2に丸められます。同様に、値-0.5、0.2および0.5は0に、値0.6、1.2および1.4は1に丸められます。

SUMMARYCONTENTS=’string’

PROC UNIVARIATEステートメントで作成される要約統計量のグループ化に使用する目次エントリを指定します。 グループエントリを抑制するには、SUMMARYCONTENTS=''を指定します。

TRIMMED=values <(<TYPE=keyword> <ALPHA=$\alpha $>)>
TRIM=values <(<TYPE=keyword> <ALPHA=$\alpha $>)>

トリム平均のテーブルを要求します。valueには、UNIVARIATEプロシジャがトリムするオブザベーションの数または割合を指定します。valueが、トリムされるオブザベーションの数nである場合、nは0から非欠損値のオブザベーション数の半数の範囲にある必要があります。valueが0から½の間にある割合pである場合、UNIVARIATEプロシジャがトリムするオブザベーションの数は、$np$以上の最小の整数値になります。ここで、nはオブザベーション数です。平均値の信頼限界およびスチューデントのt検定をテーブルに含めるには、VARDEF=のデフォルト値(DF)を使用する必要があります。トリム平均の計算の詳細は、トリム平均のセクションを参照してください。TRIMMED=オプションは、WEIGHTステートメントを使用する場合には適用されません。

TYPE=keyword

平均値の信頼限界の種類を指定します。keywordには、LOWER、UPPER、TWOSIDEDのいずれかを指定できます。デフォルト値はTWOSIDEDです。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。

VARDEF=divisor

分散および標準偏差の計算に使用する分母を指定します。デフォルトでは、VARDEF=DFです。表4.1は、divisorに使用できる値と関連する分母を示します。

表4.1: VARDEF=に使用できる値

値

分母

分母の式

DF

自由度

n - 1

N

オブザベーションの数

N

WDF

重みの合計から1を差し引いた値

$(\Sigma _ i w_ i) - 1 $

WEIGHT | WGT

重みの合計

$\Sigma _ i w_ i $


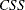プロシジャでは、分散は$\frac{CSS}{\mr{divisor}}$で計算され、ここで$CSS$は修正済平方和であり、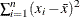$\sum _{i=1}^ n (x_ i-\bar{x})^2$に等しくなります。分析変数に重みを付加する場合は、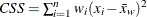$CSS = \sum _{i=1}^ n w_ i(x_ i - \bar{x}_ w)^2$になります。ここで、$\bar{x}_ w$は重み付き平均です。

デフォルト値はDFです。平均値、信頼限界およびスチューデントのt検定の標準誤差を計算するには、VARDEF=のデフォルト値を使用します。

WEIGHTステートメントとVARDEF=DFを使用するとき、分散は、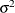$\sigma ^2$の推定値になり、ここでi番目のオブザベーションの分散は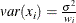$var(x_ i) = \frac{\sigma ^2}{w_ i}$であり、$w_ i$はi番目のオブザベーションの重みです。この結果は、ユニットの重みが与えられたオブザベーションの分散の推定値になります。

WEIGHTステートメントとVARDEF=WGTを使用すると、計算される分散は(nが大きい場合)漸近的に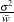$\frac{\sigma ^2}{\bar{w}}$の推定値になり、ここで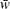$\bar{w}$は平均の重みです。この結果は、平均の重みが与えられたオブザベーションの分散の漸近推定値になります。

WINSORIZED=values <(<TYPE=keyword> <ALPHA=$\alpha $>)>
WINSOR=values <(<TYPE=keyword> <ALPHA=$\alpha $>)>

ウィンザー化平均のテーブルを要求します。valueには、ウィンザー化平均の計算にUNIVARIATEプロシジャが使用するオブザベーションの数または割合を指定します。valueがウィンザー化オブザベーションの数nである場合、nは0から非欠損値のオブザベーション数の半数の範囲にある必要があります。valueが0から½の間にある割合pである場合、UNIVARIATEプロシジャが使用するオブザベーションの数は、$np$以上の最小の整数値と等しくなり、ここでnはオブザベーション数です。平均値の信頼限界およびスチューデントのt検定をテーブルに含めるには、VARDEF=のデフォルト値(DF)を使用する必要があります。ウィンザー化平均の計算の詳細は、ウィンザー化平均のセクションを参照してください。WINSORIZED=オプションは、WEIGHTステートメントを使用する場合には適用されません。

TYPE=keyword

平均値の信頼限界の種類を指定します。keywordには、LOWER、UPPER、TWOSIDEDのいずれかを指定できます。デフォルト値はTWOSIDEDです。

ALPHA=$\alpha $

有意水準$\alpha $($100(1-\alpha )\% $信頼区間)を指定します。値$\alpha $は、0から1までの間でなければなりません。デフォルト値は0.05であり、これは95%の信頼区間を生成します。