UNIVARIATEプロシジャ

例4.22 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ

適切なデータ分布モデルを決定するには、いくつかの分布族の曲線を検討する必要があります。この例で示すように、HISTOGRAMステートメントを使用して複数の分布を当てはめ、それらの密度曲線を1つのヒストグラムに表示することができます。

溶接工程の生産品から無作為に50個の溶接済み組み立て品を選択し、各組立品の2つの金属板の間の隙間(cm)を測定します。次のステートメントは、測定値(Gap)をPlatesという名前のデータセットに保存します。

data Plates;
   label Gap = 'Plate Gap in cm';
   input Gap @@;
   datalines;
0.746  0.357  0.376  0.327  0.485 1.741  0.241  0.777  0.768  0.409
0.252  0.512  0.534  1.656  0.742 0.378  0.714  1.121  0.597  0.231
0.541  0.805  0.682  0.418  0.506 0.501  0.247  0.922  0.880  0.344
0.519  1.302  0.275  0.601  0.388 0.450  0.845  0.319  0.486  0.529
1.547  0.690  0.676  0.314  0.736 0.643  0.483  0.352  0.636  1.080
;

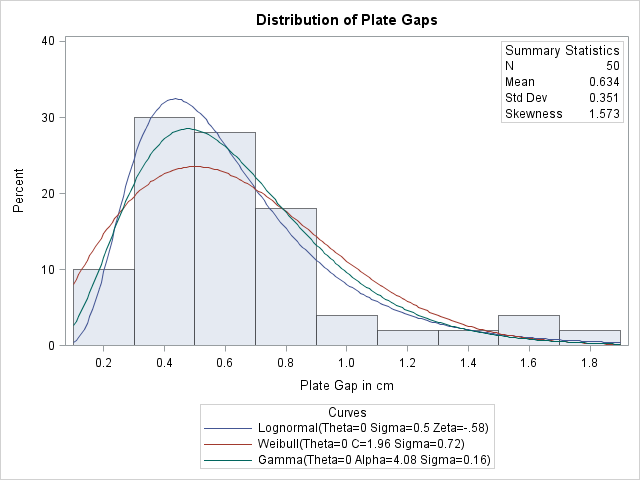
次のステートメントは3つの分布(対数正規、Weibullおよびガンマ)を当てはめ、それらの密度曲線を1つのヒストグラムに表示します。

title 'Distribution of Plate Gaps';
ods graphics on;
ods select Histogram ParameterEstimates GoodnessOfFit FitQuantiles;
proc univariate data=Plates;
   var Gap;
   histogram / midpoints=0.2 to 1.8 by 0.2
               lognormal
               weibull
               gamma
               odstitle = title;
   inset n mean(5.3) std='Std Dev'(5.3) skewness(5.3)
          / pos = ne  header = 'Summary Statistics';
run;

ODS SELECTステートメントは出力を"ParameterEstimates"、"GoodnessOfFit"および"FitQuantiles"の各テーブルに制限します。ODSテーブル名のセクションを参照してください。LOGNORMAL、WEIBULLおよびGAMMA 1次オプションは、当てはめた曲線を出力4.22.1のヒストグラムに重ねて表示するよう要求します。各曲線でしきい値パラメータは $\theta =0$ であることが前提になっています。しきい値が0ではない場合は、THETA= 2次オプションで $\theta$ を指定できます。

LOGNORMAL、WEIBULLおよびGAMMAオプションは、出力4.22.2から出力4.22.4に示されている当てはめた分布の要約も作成します。

出力4.22.2は、対数正規分布に対する3つのEDF適合度検定(Anderson-Darling、Cramér-von MisesおよびKolmogorov-Smirnov検定)を示しています。 $\alpha =0.10$ の有意水準において、尺度パラメータが $\hat{\zeta }=-0.58$ で形状パラメータが $\hat{\sigma }=0.50$ である2パラメータ対数正規分布が金属板の隙間の分布に適しているという結論が、すべての検定で支持されます。

出力4.22.1: ヒストグラムと当てはめた曲線の重ね合わせ表示

出力4.22.2: 当てはめた対数正規分布の要約

Distribution of Plate Gaps

The UNIVARIATE Procedure

Fitted Lognormal Distribution for Gap (Plate Gap in cm)

Parameters for Lognormal Distribution
Parameter	Symbol	Estimate
THRESHOLD	Theta	0
Scale	Zeta	-0.58375
SHAPE	Sigma	0.499546
MEAN		0.631932
Std Dev		0.336436

Goodness-of-Fit Tests for Lognormal Distribution
Test	Statistic		p Value
Kolmogorov-Smirnov	D	0.06441431	Pr > D	>0.150
Cramer-von Mises	W-Sq	0.02823022	Pr > W-Sq	>0.500
Anderson-Darling	A-Sq	0.24308402	Pr > A-Sq	>0.500

Quantiles for Lognormal Distribution
Percent	Quantile
Percent	Observed	Estimated
1.0	0.23100	0.17449
5.0	0.24700	0.24526
10.0	0.29450	0.29407
25.0	0.37800	0.39825
50.0	0.53150	0.55780
75.0	0.74600	0.78129
90.0	1.10050	1.05807
95.0	1.54700	1.26862
99.0	1.74100	1.78313

出力4.22.3: 当てはめたWeibull分布の要約

Distribution of Plate Gaps

The UNIVARIATE Procedure

Fitted Weibull Distribution for Gap (Plate Gap in cm)

Parameters for Weibull Distribution
Parameter	Symbol	Estimate
THRESHOLD	Theta	0
Scale	Sigma	0.719208
SHAPE	C	1.961159
MEAN		0.637641
Std Dev		0.339248

Goodness-of-Fit Tests for Weibull Distribution
Test	Statistic		p Value
Cramer-von Mises	W-Sq	0.15937281	Pr > W-Sq	0.016
Anderson-Darling	A-Sq	1.15693542	Pr > A-Sq	<0.010

Quantiles for Weibull Distribution
Percent	Quantile
Percent	Observed	Estimated
1.0	0.23100	0.06889
5.0	0.24700	0.15817
10.0	0.29450	0.22831
25.0	0.37800	0.38102
50.0	0.53150	0.59661
75.0	0.74600	0.84955
90.0	1.10050	1.10040
95.0	1.54700	1.25842
99.0	1.74100	1.56691

出力4.22.3は、Weibull分布に対する2つのEDF適合度検定(Anderson-DarlingおよびCramér-von Mises検定)を示しています。EDF検定のp値はすべて0.10より小さく、このデータがWeibullモデルをサポートしないことを示しています。

出力4.22.4: 当てはめたガンマ分布の要約

Distribution of Plate Gaps

The UNIVARIATE Procedure

Fitted Gamma Distribution for Gap (Plate Gap in cm)

Parameters for Gamma Distribution
Parameter	Symbol	Estimate
THRESHOLD	Theta	0
Scale	Sigma	0.155198
SHAPE	Alpha	4.082646
MEAN		0.63362
Std Dev		0.313587

Goodness-of-Fit Tests for Gamma Distribution
Test	Statistic		p Value
Kolmogorov-Smirnov	D	0.09695325	Pr > D	>0.250
Cramer-von Mises	W-Sq	0.07398467	Pr > W-Sq	>0.250
Anderson-Darling	A-Sq	0.58106613	Pr > A-Sq	0.137

Quantiles for Gamma Distribution
Percent	Quantile
Percent	Observed	Estimated
1.0	0.23100	0.13326
5.0	0.24700	0.21951
10.0	0.29450	0.27938
25.0	0.37800	0.40404
50.0	0.53150	0.58271
75.0	0.74600	0.80804
90.0	1.10050	1.05392
95.0	1.54700	1.22160
99.0	1.74100	1.57939

出力4.22.4は、ガンマ分布に対する3つのEDF適合度検定(Anderson-Darling、Cramér-von MisesおよびKolmogorov-Smirnov検定)を示しています。 $\alpha =0.10$ の有意水準において、尺度パラメータが $\sigma =0.16$ で形状パラメータが $\alpha =4.08$ であるガンマ分布が金属板の隙間の分布に適しているという結論が、すべての検定で支持されます。

この分析に基づき、当てはめた対数正規分布と当てはめたガンマ分布の2つのモデルが金属板の隙間の分布に適しています。

この例のサンプルプログラムuniex13.sasは、Base SASソフトウェアのSASサンプルライブラリに含まれています。