UNIVARIATEプロシジャ
- 概要
-
入門ガイド

-
構文

-
詳細
 欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース
欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース -
例
 複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成
複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成 - リファレンス
例4.31 対数正規分位点プロットからの3パラメータの推定
この例は例4.30の続きで、3パラメータ対数正規分布の形状パラメータ、しきい値パラメータ、尺度パラメータ、理論パーセント点を推定する方法を示しています。
3パラメータ対数正規分布はしきい値パラメータ 、尺度パラメータ
、尺度パラメータ および形状パラメータ
および形状パラメータ に依存します。SIGMA= 2次オプションを使用してさまざまな
に依存します。SIGMA= 2次オプションを使用してさまざまな の値を指定した一連の対数正規Q-Qプロットから、
の値を指定した一連の対数正規Q-Qプロットから、 を推定できます。点のパターンが線形になる値が
を推定できます。点のパターンが線形になる値が の推定値になります。次に、点のパターンの切片と傾きから、しきい値パラメータと尺度パラメータを推定できます。次のステートメントは、
の推定値になります。次に、点のパターンの切片と傾きから、しきい値パラメータと尺度パラメータを推定できます。次のステートメントは、 値に0.2、0.5および0.8を使用して、出力4.31.1、出力4.31.2および出力4.31.3にある一連のプロットをそれぞれ作成します。
値に0.2、0.5および0.8を使用して、出力4.31.1、出力4.31.2および出力4.31.3にある一連のプロットをそれぞれ作成します。
symbol v=plus;
title 'Lognormal Q-Q Plot for Diameters';
ods graphics off;
proc univariate data=Measures noprint;
qqplot Diameter / lognormal(sigma=0.2 0.5 0.8)
square;
run;
注:対数正規Q-Qプロットの形状パラメータ の値は、SIGMA=オプションまたはその別名のSHAPE=オプションで指定する必要があります。
の値は、SIGMA=オプションまたはその別名のSHAPE=オプションで指定する必要があります。
 =0.2)
=0.2) 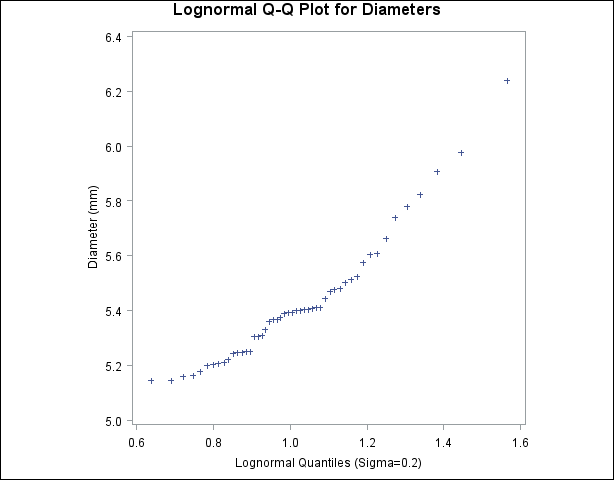
 =0.5)
=0.5) 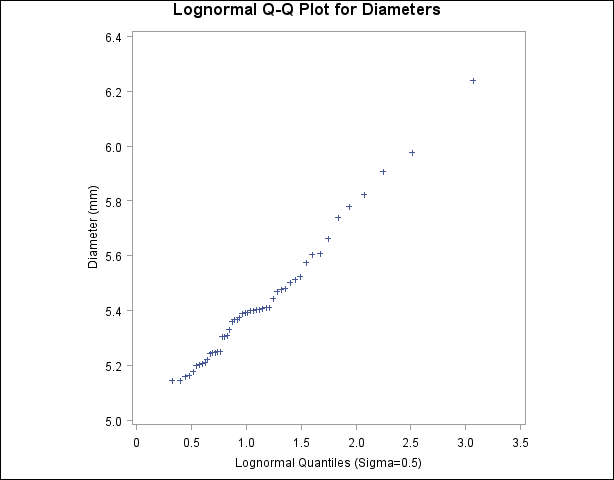
 =0.8)
=0.8) 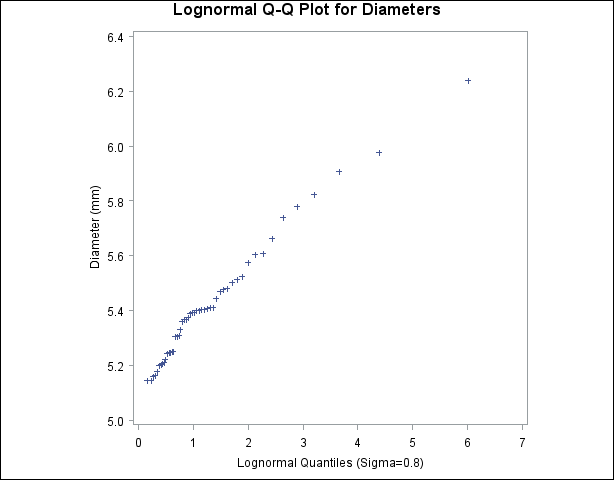
出力4.31.2のプロットに最も線形に近い点のパターンが表示され、 による当てはめがデータ分布に対して適切であることを示しています。
による当てはめがデータ分布に対して適切であることを示しています。
この対数正規分布によるデータの密度関数は次のようになります。
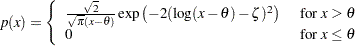 |
プロットの点は、切片が 、傾きが
、傾きが の線上またはその近くにプロットされます。出力4.31.2に基づき、
の線上またはその近くにプロットされます。出力4.31.2に基づき、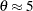 および
および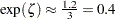 で、
で、 が求められます。
が求められます。
SIGMA=、THETA=およびZETA=の各オプションを併用して、参照線を要求することもできます。次のステートメントは出力4.31.4の対数正規Q-Qプロットを作成します。
symbol v=plus;
title 'Lognormal Q-Q Plot for Diameters';
ods graphics off;
proc univariate data=Measures noprint;
qqplot Diameter / lognormal(theta=5 zeta=est sigma=est
color=black l=2)
square;
run;
出力4.31.1~出力4.31.3は、しきい値パラメータ が0に等しくないことを示しています。THETA=5の指定はデフォルト値の0より優先されます。SIGMA=ESTおよびZETA=ESTの2次オプションは、標本平均と標準偏差による
が0に等しくないことを示しています。THETA=5の指定はデフォルト値の0より優先されます。SIGMA=ESTおよびZETA=ESTの2次オプションは、標本平均と標準偏差による と
と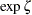 の推定値を要求しています。
の推定値を要求しています。
 =est、
=est、 =est、
=est、 =5)
=5) 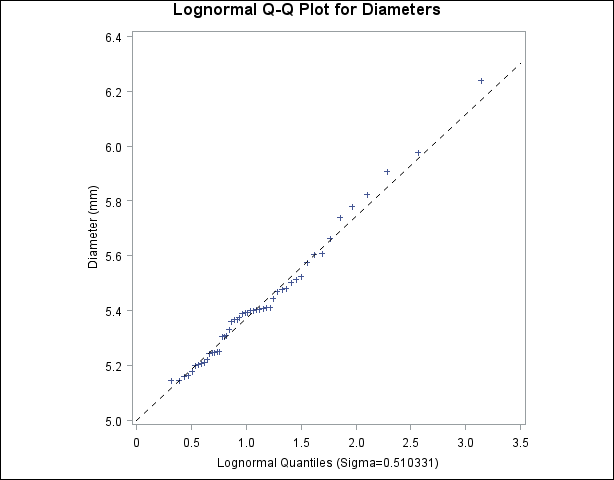
出力4.31.2のプロットから、 は0.51と推定できます。これは出力4.31.2のプロットから導き出される推定値0.5と一致しています。例4.32では、対数正規Q-Qプロットを使用してパーセント点を推定する方法を示しています。
は0.51と推定できます。これは出力4.31.2のプロットから導き出される推定値0.5と一致しています。例4.32では、対数正規Q-Qプロットを使用してパーセント点を推定する方法を示しています。
この例のサンプルプログラムuniex18.sasは、Base SASソフトウェアのSASサンプルライブラリに含まれています。