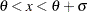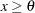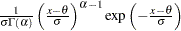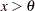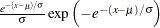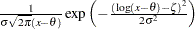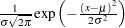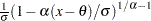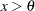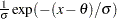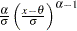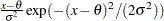UNIVARIATEプロシジャ
- 概要
-
入門ガイド

-
構文

-
詳細
 欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース
欠損値 丸め 記述統計量 モードの計算 パーセント点の計算 位置の検定 正規分布のパラメータに対する信頼限界 ロバスト推定量 ラインプリンタプロットの作成 高解像度グラフの作成 CLASSステートメントを使用した比較プロットの作成 インセットの配置 当てはめた連続分布の計算式 適合度検定 核密度推定 Q-Qプロットと確率プロットの作成 Q-Qプロットと確率プロットの解釈 確率プロットとQ-Qプロットの分布 Q-Qプロットを使用した形状パラメータの推定 Q-Qプロットを使用した位置パラメータと尺度パラメータの推定 Q-Qプロットを使用したパーセント点の推定 入力データセット OUTPUTステートメントのOUT=出力データセット OUTHISTOGRAM=出力データセット OUTKERNEL=出力データセット OUTTABLE=出力データセット 要約統計量のテーブル ODSテーブル名 当てはめた分布のODSテーブル ODS Graphics 計算リソース -
例
 複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成
複数の変数に対する記述統計量の計算 モードの計算 極値のオブザベーションと極値の表示 度数表の作成 ラインプリンタ出力プロットの作成 FREQ変数を使用したデータセットの分析 OUT=出力データセットへの要約統計量の保存 出力データセットへのパーセント点の保存 平均、標準偏差、分散に対する信頼限界の計算 分位点とパーセント点に対する信頼限界の計算 ロバスト推定の計算 位置の検定 対応のあるデータを使用した符号検定の実行 ヒストグラムの作成 一元比較ヒストグラムの作成 二元比較ヒストグラムの作成 記述統計量を含むインセットの追加 ヒストグラムのビン幅の指定 正規曲線をヒストグラムに追加する 当てはめた正規曲線を比較ヒストグラムに追加する ベータ曲線の当てはめ 対数正規曲線、Weibull曲線、ガンマ曲線の当てはめ 核密度推定の計算 3パラメータ対数正規曲線の当てはめ 折り重ねられた正規曲線の追加表示 対数正規確率プロットの作成 対数正規分布の当てはめを表示するヒストグラムの作成 正規確率プロットの作成 分布の参照線の追加 正規確率プロットの解釈 対数正規確率プロットから3パラメータを推定する 対数正規確率プロットからパーセント点を推定する 対数正規確率プロットからパラメータを推定する Weibull分布の分位点プロットの比較 累積分布プロットの作成 P-Pプロットの作成 - リファレンス
| 確率プロットとQ-Qプロットの分布 |
PROBPLOTおよびQQPLOTステートメントを使用して、表4.116に要約されている理論分布に基づく、確率プロットとQ-Qプロットを要求できます。
パラメータ |
||||||
|---|---|---|---|---|---|---|
分布 |
密度関数 |
Range |
ロケーション |
尺度 |
形状 |
|
ベータ |
|
|
|
|
|
|
指数 |
|
|
|
|
||
ガンマ |
|
|
|
|
|
|
Gumbel |
|
すべて |
|
|
||
対数正規 |
|
|
|
|
|
|
(3つのパラメータ) |
||||||
正規 |
|
すべて |
|
|
||
一般化 |
|
|
|
|
|
|
パレート |
|
|
||||
べき関数 |
|
|
|
|
|
|
レイリー |
|
|
|
|
||
Weibull |
|
|
|
|
|
|
(3つのパラメータ) |
||||||
Weibull |
|
|
|
|
|
|
(2パラメータ) |
(既知) |
|||||
これらの分布は、それぞれ、BETA、EXPONENTIAL、GAMMA、PARETO、GUMBEL、LOGNORMAL、NORMAL、POWER、RAYLEIGH、WEIBULL、WEIBULL2の各オプションで要求できます。分布オプションを指定しなかった場合、正規確率プロットまたは正規Q-Qプロットが作成されます。
次のセクションで、これらの分布に基づくQ-Qプロットの作成の詳細について説明します。確率プロットは、水平軸の目盛りがパーセント点単位であることを除いて、同じように作成されます。
ベータ分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点 に対してプロットされます。ここで、
に対してプロットされます。ここで、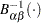 は逆正規化された不完全なベータ関数、
は逆正規化された不完全なベータ関数、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 および
および はベータ分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
はベータ分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
ALPHA= およびBETA=
およびBETA= のプロットのパターンは、データが次の特定の密度関数のベータ分布である場合、切片が
のプロットのパターンは、データが次の特定の密度関数のベータ分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
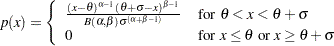 |
ここで および
および
 下側いき値パラメータ
下側いき値パラメータ  尺度パラメータ
尺度パラメータ
 1番目の形状パラメータ
1番目の形状パラメータ
 2番目の形状パラメータ
2番目の形状パラメータ
指数分布
プロットを作成するには、オブザベーションを昇順に並べ替え、 番目のオブザベーションがパーセント点
番目のオブザベーションがパーセント点 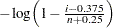 に対してプロットされるようにします。ここで、
に対してプロットされるようにします。ここで、 は欠損値を含まないオブザベーションの数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
は欠損値を含まないオブザベーションの数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
プロットのパターンは、データが次の特定の密度関数の指数分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
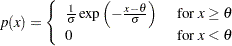 |
ここで、 はしきい値パラメータであり、
はしきい値パラメータであり、 は正の尺度パラメータです。
は正の尺度パラメータです。
ガンマ分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は逆正規化された不完全なガンマ関数、
は逆正規化された不完全なガンマ関数、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 はガンマ分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
はガンマ分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
ALPHA= のプロットのパターンは、データが次の特定の密度関数のガンマ分布である場合、切片が
のプロットのパターンは、データが次の特定の密度関数のガンマ分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
 |
ここで、
 いき値パラメータ
いき値パラメータ  尺度パラメータ
尺度パラメータ
 形状パラメータ
形状パラメータ
Gumbel分布
プロットを作成するには、オブザベーションを昇順に並べ替え、 番目のオブザベーションがパーセント点
番目のオブザベーションがパーセント点  に対してプロットされるようにします。ここで、
に対してプロットされるようにします。ここで、 は欠損値を含まないオブザベーションの数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
は欠損値を含まないオブザベーションの数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
プロットのパターンは、データが次の特定の密度関数のGumbel分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
 |
 位置パラメータ
位置パラメータ  尺度パラメータ
尺度パラメータ
対数正規分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は逆累積標準正規分布、
は逆累積標準正規分布、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 は対数正規分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
は対数正規分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
SIGMA= のプロットのパターンは、データが次の特定の密度関数の対数正規分布である場合、切片が
のプロットのパターンは、データが次の特定の密度関数の対数正規分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
 |
説明
 いき値パラメータ
いき値パラメータ  尺度パラメータ
尺度パラメータ  形状パラメータ
形状パラメータ
正規分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点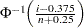 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は逆累積標準正規分布、
は逆累積標準正規分布、 は非欠損オブザベーション数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
は非欠損オブザベーション数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
プロットの点のパターンは、データが次の特定の密度関数の正規分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
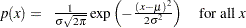 |
ここで、 は平均で、
は平均で、 は標準偏差(
は標準偏差(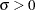 )です。
)です。
一般化パレート分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点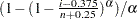 (
(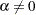 )または
)または (
(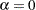 )に対してプロットされます。ここで、
)に対してプロットされます。ここで、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 は一般化パレート分布の形状パラメータです。水平軸上の目盛りはパーセント単位になります。
は一般化パレート分布の形状パラメータです。水平軸上の目盛りはパーセント単位になります。
ALPHA= のプロットの点のパターンは、データが次の特定の密度関数の一般化パレート分布である場合、切片が
のプロットの点のパターンは、データが次の特定の密度関数の一般化パレート分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
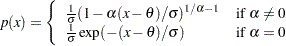 |
ここで、 しきい値パラメータ
しきい値パラメータ 尺度パラメータ
尺度パラメータ
 形状パラメータ
形状パラメータ
べき関数分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点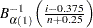 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は逆正規化された不完全なベータ関数、
は逆正規化された不完全なベータ関数、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 はベータ分布の1番目の形状パラメータ、
はベータ分布の1番目の形状パラメータ、 はベータ分布の2番目の形状パラメータです。水平軸の目盛りはパーセント点単位になります。
はベータ分布の2番目の形状パラメータです。水平軸の目盛りはパーセント点単位になります。
ALPHA= のプロットの点のパターンは、データが次の特定の密度関数のべき関数分布である場合、切片が
のプロットの点のパターンは、データが次の特定の密度関数のべき関数分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
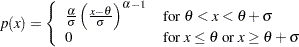 |
説明
 いき値パラメータ
いき値パラメータ  形状パラメータ
形状パラメータ
 形状パラメータ
形状パラメータ
レイリー分布
プロットを作成するには、オブザベーションを昇順に並べ替え、 番目のオブザベーションがパーセント点
番目のオブザベーションがパーセント点 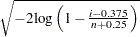 に対してプロットされるようにします。ここで、
に対してプロットされるようにします。ここで、 は欠損値を含まないオブザベーションの数です。水平軸上の目盛りはパーセント単位になります。
は欠損値を含まないオブザベーションの数です。水平軸上の目盛りはパーセント単位になります。
プロットの点のパターンは、データが次の特定の密度関数のレイリー分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
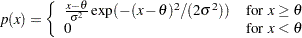 |
ここで、 はしきい値パラメータであり、
はしきい値パラメータであり、 は正の尺度パラメータです。
は正の尺度パラメータです。
3パラメータWeibull分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、 番目の並べ替えられたオブザベーションが分位点
番目の並べ替えられたオブザベーションが分位点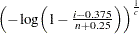 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は非欠損オブザベーション数、
は非欠損オブザベーション数、 はWeibull分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
はWeibull分布の形状パラメータです。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
C= のプロットのパターンは、データが次の特定の密度関数のWeibull分布である場合、切片が
のプロットのパターンは、データが次の特定の密度関数のWeibull分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
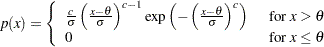 |
ここで、
 いき値パラメータ
いき値パラメータ  尺度パラメータ
尺度パラメータ
 形状パラメータ
形状パラメータ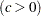
例l4.34を参照してください。
2パラメータWeibull分布
プロットを作成するため、オブザベーションは昇順に並べ替えられ、シフトした 番目の並べ替えられたオブザベーション
番目の並べ替えられたオブザベーション の対数(
の対数(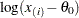 で表されます)が分位点
で表されます)が分位点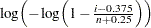 に対してプロットされます。ここで、
に対してプロットされます。ここで、 は非欠損オブザベーション数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
は非欠損オブザベーション数です。確率プロットでは、水平軸上の目盛りはパーセント単位になります。
3パラメータWeibull分位点と異なり、前の式は分布パラメータを含みません。このため、C=形状パラメータはWEIBULL2分布オプションでは必須ではありません。
THETA= のプロットのパターンは、データが次の特定の密度関数のWeibull分布である場合、切片が
のプロットのパターンは、データが次の特定の密度関数のWeibull分布である場合、切片が および傾きが
および傾きが の線形になりやすくなります。
の線形になりやすくなります。
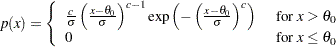 |
ここで、
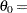 既知の下限しきい値
既知の下限しきい値  尺度パラメータ
尺度パラメータ
 形状パラメータ
形状パラメータ
例l4.34を参照してください。