FREQプロシジャ

正確な統計量

正確な統計量は、漸近仮定が満たされないために、漸近p値が真のp値の近い近似とならないような場合に役立ちます。標準漸近方式では、標本サイズが十分に大きい場合に検定統計量は特定の分布に従うという仮定を置きます。標本サイズが大きくない場合、漸近p値が正確なp値から大きく異なっているため、漸近結果が妥当でないことがあります。データの分布が疎である場合や片寄った分布である場合にも、漸近結果が信頼できないことがあります。 詳細は、Agresti (2007)およびBishop, Fienberg, and Holland (1975)を参照してください。正確な計算は、Agresti (1992)により見直された、分割表に対する条件付き推定の統計理論に基づいています。

正確なp値の計算に加えて、FREQプロシジャは、モンテカルロシミュレーションによる正確なp値を推定するオプションを提供します。これは、正確な計算をするためには大量の時間とメモリが必要となるが、漸近近似では十分でないような大きな問題に役立ちます。

正確な統計量は、多くのFREQプロシジャの検定で利用できます。一元表の場合、FREQプロシジャは、二項比率検定およびカイ2乗適合度検定のp値を計算します。正確な(Clopper-Pearson)信頼限界は、二項比率で使用できます。二元表の場合、FREQプロシジャは、Pearsonのカイ2乗、尤度比カイ2乗、Mantel-Haenszelのカイ2乗、Fisherの正確検定、Jonckheere-Terpstra検定、Cochran-Armitageの傾向検定のような各検定の正確なp値を計算します。また、FREQプロシジャは、KendallのTau-b、StuartのTau-c、Somersの$D (C|R)$、Somersの$D (R|C)$、Pearson相関係数、Spearman相関係数、単純カッパ係数、重み付きカッパ係数のような統計量の正確な値も計算します。 $2 \times 2$表の場合、FREQプロシジャは、McNemarの正確検定と、オッズ比の正確な信頼限界を計算します。FREQプロシジャは、比率(リスク)の差および相対リスクの正確な無条件の信頼限界も計算します。層化された$2 \times 2$表の場合、FREQプロシジャは、オッズ比の等質性に対するZelenの正確検定、共通オッズ比の正確な信頼限界、共通オッズ比の正確検定を提供します。

次の各セクションでは、正確な計算のアルゴリズムの要約と、FREQプロシジャが計算する正確なp値の定義を示し、計算リソース要件やモンテカルロ推定オプションについて説明します。

計算アルゴリズム

FREQプロシジャは、Mehta and Patel (1983)によって開発されたネットワークアルゴリズムを使用して、一般的な$R \times C$表の正確なp値を計算します。非常に時間がかかる上に小さな問題にしか適さない直接的な列挙に比べて、このアルゴリズムには大きな利点があります。正確なp値の計算方法についてはAgresti (1992)を参照してください。ネットワークアルゴリズムの性能に関する詳細は、Mehta, Patel, and Tsiatis (1984)およびMehta, Patel, and Senchaudhuri (1991)を参照してください。

与えられた分割表の参照集合は、観測された行および列の周辺合計を含むすべての分割表の集合になります。この参照集合に対応して、ネットワークアルゴリズムは、複数のステージ内のノードから構成される指示された非環式ネットワークを形成します。ネットワークを通じたパスは、参照集合内にある1つの表に対応します。ノード間の距離は、ネットワークを通じたパスの合計距離が検定統計量の対応する値となるように定義されます。各ノードで、このアルゴリズムにより、同ノードを経由するすべてのパスに関して、最短および最長パス距離が計算されます。増加する行スコアおよび列スコアを乗じたセル度数の線形の組み合わせとして表される統計量の場合、FREQプロシジャは、Agresti, Mehta, and Patel (1990)のアルゴリズムを使用して最短および最長パス距離を計算します。それ以外の形式の統計量の場合、FREQプロシジャは、Valz and Thompson (1994)の手法に従うことで、最長パスの上限と最短パスの下限を計算します。

あるノードの最長および最短パス距離または上限下限を検定統計量の値と比較することにより、そのノードを通じたすべてのパスがp値に寄与するか、それともそのノードを通じたいかなるパスもp値に寄与しない、あるいはどちらの状態も起こらないのいずれかが決定されます。そのノードを通じたすべてのパスが寄与する場合、それに従ってp値がインクリメントされ、それらのパスは以降の分析から除外されます。いかなるパスも寄与しない場合、それらのパスは分析から除外されます。それ以外の場合、このアルゴリズムは、そのノードと関連するパスを処理し続けます。 すべてのノードが説明された時点で、このアルゴリズムは完了します。

ネットワークアルゴリズムの適用において、FREQプロシジャは完全な数値精度を使用して、すべての統計量、行スコアと列スコア、および計算に関係するその他の数量を表します。アルゴリズムの速度とメモリ要件を改善するために丸めを使用することは可能ですが、その結果としてp値の精度が低下するため、FREQプロシジャは丸めを使用しません。

一元表の場合、FREQプロシジャは、Radlow and Alf (1975)の方法を使用して、正確なカイ2乗適合度検定を計算します。FREQプロシジャは、観測された合計標本サイズとカテゴリ数を持つすべての可能な一元表を生成します。個々の可能な表に関して、FREQプロシジャは、そのカイ2乗値を、観測された表の値と比較します。ある表のカイ2乗値が観測されたカイ2乗値以上である場合、FREQプロシジャは、そのテーブルの確率だけ正確なp値をインクリメントします。この確率は、多元度数分布を使用することにより帰無仮説の下で計算されます。デフォルトでは、この帰無仮説は、すべてのカテゴリが等しい比率を持つことを主張します。TABLESステートメントでTESTP=またはTESTF=オプションを使用して帰無仮説の比率や度数を指定すると、FREQプロシジャは、その帰無仮説に基づいて正確なカイ2乗検定を計算します。

その他の正確な計算については、各統計量について説明したセクションを参照してください。FREQプロシジャによる二項比率の正確な信頼限界や検定の計算方法についての詳細は、二項比率のセクションを参照してください。$2 \times 2$表のオッズ比に対する正確な信頼限界の計算方法については、2x2表に対するオッズ比と相対リスクのセクションを参照してください。また、リスク差の正確な条件なしの信頼限界、共通オッズ比の正確な信頼限界、オッズ比の等質性に対するZelenの正確検定の各セクションも参照してください。

p値の定義

FREQプロシジャにおける複数の検定では、検定統計量は非負であり、検定統計量の大きい値は帰無仮説からの逸脱を意味します。このような無方向性の検定には、Pearsonカイ2乗、尤度比カイ2乗、Mantel-Haenszelのカイ2乗、$2 \times 2$より大きい表のFisherの正確検定、McNemarの検定、一元カイ2乗適合度検定などが含まれます。無方向性の検定の正確なp値は、観測された検定統計量の値以上の検定統計量を持つ表における確率の合計になります。

片側または両側の対立仮説の検定に適している検定は、上記以外にも存在します。 たとえば、真のパラメータが0に等しい($T = 0$)という帰無仮説を検定する場合、対立仮説は片側の($T \leq 0$、または$T \geq 0$)になるか、または両側の($T \neq 0$)になります。このような検定には、Pearson相関係数、Spearman相関係数、Jonckheere-Terpstra検定、Cochran-Armitageの傾向検定、単純カッパ係数、重み付きカッパ係数などが含まれます。これらの検定の場合、FREQプロシジャは、検定統計量の観測値が期待値より大きいならば、右側のp値を表示します。右側のp値は、観測された検定統計量値以上の検定統計量を持つ表における確率の合計になります。それ以外の場合、観測された検定統計量が期待値以下であるならば、FREQプロシジャは左側のp値を表示します。左側のp値は、観測された検定統計量値以下の検定統計量を持つ表における確率の合計になります。 片側のp値$P_{1}$は次のように計算されます。

\begin{equation*} P_1 = \begin{cases} \mr{Prob} (~ \mbox{Test Statistic} \geq t~ ) \quad \mr{if} \hspace{.1in} t > \mr{E}_0(T) \\ \mr{Prob} (~ \mbox{Test Statistic} \leq t~ ) \quad \mr{if} \hspace{.1in} t \leq \mr{E}_0(T) \\ \end{cases}\end{equation*}

ここで、tは検定統計量の観測値、$\mr {E}_0(T)$は帰無仮説の下での検定統計量の期待値です。FREQプロシジャは、両側のp値を、片側のpの合計および分布の反対側の裾にある対応する領域(期待値から等距離にある領域)としても計算します。両側のp値$P_{2}$は次のように計算されます。

\[ P_{2} = \mr{Prob} \left( ~ | \mbox{Test Statistic} - \mr{E}_0(T) | \geq | t - \mr{E}_0(T) | \right) \]

EXACTステートメントでPOINTオプションを指定すると、FREQプロシジャは正確検定の正確な点確率を提供します。正確な点確率とは、検定統計量が観測値と等しくなる正確な確率です。

EXACTステートメントでMIDPオプションを指定すると、FREQプロシジャは正確なmid-p値を提供します。正確なmid p値は、正確なp値から正確な点確率の半分を差し引いた値として定義されます。これは右側検定の$\mr{Prob} ( \mbox{Test Statistic} \geq t )$と$\mr{Prob} ( \mbox{Test Statistic} > t )$の平均に等しくなります。正確なmid p値は、未調整の正確なp値よりも小さくてより保守的ではありません。詳細は、Agresti (2013, section 1.1.4)およびHirji (2006, sections 2.5 and 2.11.1)を参照してください。

計算リソース

FREQプロシジャは、比較的高速かつ効率的なアルゴリズムを使用して、正確な計算を行います。これらの近年開発されたアルゴリズムを性能が改善されたコンピュータ上で使用することにより、以前は漸近方式のみが適用されていたデータセットに対して現在では正確検定が行えるようになりました。それにもかかわらず、コンピュータ上で利用可能な速度とメモリによっては、正確な計算を行うのに法外な量の時間とメモリを必要とする大きな問題は依然として存在しています。大きな問題の場合、正確検定が本当に必要であるかどうか、漸近方式を使うことにより大幅に少ない時間とメモリで正確な結果にきわめて近い結果を提供できるかどうかについて検討する必要があります。漸近検定がそのような大きな問題に妥当でない場合、正確なp値のモンテカルロ推定の使用を検討します。詳細は、モンテカルロ推定のセクションを参照してください。

特定の問題の正確なp値を計算するのにどれくらいの量の時間やメモリが必要となるかを事前に予測できるような公式は存在しません。必要となる時間やメモリは、実施する検定の種類、合計標本サイズ、行と列の数、表セル内へのオブザベーションの具体的な配列のような複数の要因により決定されます。 一般的に、(合計標本サイズ、行数、列数などが)大きな問題ほど、より多くの時間とメモリを必要とする傾向があります。また、合計標本サイズが固定されている場合、行数や列数が増えるほど、必要となる時間とメモリが増加する傾向があります。これは、行数や列数の増加が、参照集合内の表の数に対応しているためです。さらに、標本サイズが固定されている場合、行および列の周辺合計の等質性が高くなるほど、必要となる時間とメモリが増加します。詳細は、Agresti, Mehta, and Patel (1990)およびGail and Mantel (1977)を参照してください。

FREQプロシジャが正確なp値を計算している任意の時点で同計算を中止するには、システム中断のショートカットキー(使用しているシステムのSAS 使用の手引きを参照)を押した後、計算の中止を選択します。正確な計算が中止されると、FREQプロシジャは残りのタスクを完了します。同プロシジャは要求された出力を生成し、終了時間までに計算が完了しなかった正確なp値に対して欠損値を報告します。

また、EXACTステートメントでMAXTIME=オプションを指定すると、FREQプロシジャが正確な計算に使用する時間量を制限できます。 MAXTIME=オプションには、FREQプロシジャが正確なp値の計算に使用できるクロック時間(秒)の最大値を指定します。FREQプロシジャが正確なp値の計算をこの時間内に完了できなかった場合、同プロシジャは計算を中止した後、その他の残りのタスクを完了します。

モンテカルロ推定

EXACTステートメントでMCオプションを指定すると、FREQプロシジャは、正確なp値を直接計算する代わりに、正確なp値のモンテカルロ推定値を計算します。モンテカルロ推定値は、正確な計算をするためには大量の時間とメモリが必要となるが、漸近近似では十分でないような、大きな問題の場合に役立ちます。各モンテカルロ推定値の精度を記述する場合、FREQプロシジャは漸近標準誤差と$100(1-\alpha )$%の信頼限界を提供します。信頼水準$\alpha $は、EXACTステートメントのALPHA=オプションにより定義されます。この値はデフォルトで0.01であり、99%の信頼限界を生成します。 EXACTステートメントのN=nオプションは、FREQプロシジャがモンテカルロ推定に使用する標本数を指定します。デフォルトでは標本数は10000になります。nに大きい値を指定するほど、モンテカルロ推定値の精度を高めることができます。nの値が大きいほど、より多くの標本が生成されるため、計算時間は増加します。または、nに小さい値を指定することで、計算時間を短縮できます。

正確なp値のモンテカルロ推定値を計算する場合、FREQプロシジャは、観測された表と同じ合計標本サイズ、行合計、列合計を持つ表のランダムな標本を生成します。FREQプロシジャは、Agresti, Wackerly, and Boyett (1979)のアルゴリズムを使用します。このアルゴリズムは、表を表の超幾何確率に比例させて、周辺度数を条件として生成します。個々の標本表に関して、FREQプロシジャは検定統計量の値を計算し、その値を観測された表の値と比較します。 右側のp値を推定する場合、FREQプロシジャは、観測された検定統計量以上の検定統計量を持つすべての標本表をカウントします。 この結果、p値の推定値は、これらの表の数を標本化された表の合計数で割った値に等しくなります。

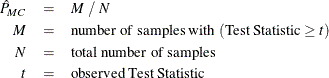
\begin{eqnarray*} \hat{P}_{\mi{MC}} & = & M ~ / ~ N \\ M & = & \mbox{number of samples with } (\mbox{Test Statistic} \geq t) \\ N & = & \mbox{total number of samples} \\ t & = & \mbox{observed Test Statistic} \end{eqnarray*}

FREQプロシジャは、左側および両側のp値の推定値を同様の方法で計算します。左側のp値の場合、FREQプロシジャは、個々の標本化された表の検定統計量が観測された検定統計量以下であるかどうかを評価します。両側のp値の場合、FREQプロシジャは、$P_{2}$の式(p値の定義セクションで示されているもの)に従って標本検定統計量を調べます。

変数Mは、N回の試行で成功確率がpである二項分布変数です。この結果、モンテカルロ推定値の漸近標準誤差は次のようになります。

\[ \mr{se}(\hat{P}_{\mi{MC}}) = \sqrt {~ \hat{P}_{\mi{MC}} ~ ( 1 - \hat{P}_{\mi{MC}}) ~ / ~ (N-1) } \]

FREQプロシジャは、p値の漸近信頼限界を次の式に従って構成します。

\[ \hat{P}_{\mi{MC}} ~ \pm ~ \left( z_{\alpha /2} ~ \times ~ \mr{se}(\hat{P}_{\mi{MC}}) \right) \]

ここで、$z_{\alpha /2}$は、標準正規分布の $100(1-\alpha /2)$番目のパーセント点であり、信頼水準$\alpha $は、EXACTステートメントのALPHA= オプションにより決定されます。

モンテカルロ推定値$\hat{P}_{\mi {MC}}$が0に等しい場合、FREQプロシジャはp値の信頼限界を次のように計算します。

\[ ( ~ 0, ~ ~ 1 - \alpha ^{(1/N)} ~ ) \]

モンテカルロ推定値$\hat{P}_{MC}$が1に等しい場合、FREQプロシジャは信頼限界を次のように計算します。

\[ ( ~ \alpha ^{(1/N)}, ~ ~ 1 ~ ) \]