FREQプロシジャ

二項比率

TABLESステートメントでBINOMIALオプションを指定すると、FREQプロシジャは一元表の二項比率を計算します。デフォルトでは、これは、出力に表示される最初の変数水準のオブザベーションの割合になります。なお、二項比率の別の水準を指定するには、LEVEL=オプションを使用します。二項比率は次のように計算されます。

$\hat{p} = n_{1} ~ / ~ n$

ここで、 $n_{1}$ は最初の(または指定された)水準の度数であり、nは一元表の合計度数です。二項比率の標準誤差は次のように計算されます。

$\mr{se}(\hat{p}) = \sqrt { \hat{p} ~ (1 - \hat{p} ) ~ / ~ n }$

二項比率の信頼限界

FREQプロシジャは、二項比率のWald信頼限界および正確な(Clopper-Pearson)信頼限界を提供します。または、BINOMIAL(CL=)オプションを指定して、二項比率の信頼限界の種類としてAgresti-Coull、Blaker、Jeffreys、正確なmid-p、尤度比、ロジット、Wilson (スコア)を要求することもできます。詳細は、信頼限界の各種類の説明で示されているリファレンスに加えて、Brown, Cai, and DasGupta (2001)、Agresti and Coull (1998)、およびNewcombe (1998b)を参照してください。

Wald信頼限界

Wald漸近信頼限界は、二項分布の正規近似に基づきます。FREQプロシジャは、二項比率のWald信頼限界を次のように計算します。

$\hat{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\hat{p}) ~ )$

ここで、 $z_{\alpha /2}$ は、標準正規分布の $100(1-\alpha /2)$ 番目のパーセント点です。信頼水準 $\alpha$ は、ALPHA=オプションにより定義されます。この値はデフォルトで0.05であり、99%の信頼限界を生成します。

CL=WALD(CORRECT)またはCORRECT binomial-optionを指定すると、FREQプロシジャは、Wald漸近信頼限界に $1/2n$ の連続性補正を含めます。この補正の目的は、正規近似と、離散的な二項分布との間の差異を調整することにあります。詳細は、Fleiss, Levin, and Paik (2003)を参照してください。二項比率の連続性補正Wald信頼限界は、次のように計算されます。

$\hat{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \mr{se}(\hat{p}) ~ + ~ (1/2n) ~ )$

正確な(Clopper-Pearson)信頼限界

二項比率の正確な(Clopper-Pearson)信頼限界は、二項分布に基づく等尾部検定を反転することにより構成されます。この方法は、Clopper and Pearson (1934)により完成されたものです。正確な信頼限界 $p_{\mi {L}}$ および $p_{\mi {U}}$ は、 $n_1 = 1, 2, \ldots n-1$ において、次の方程式を満たします。

$\begin{eqnarray*} \sum _{x=n_1}^{n} \binom {n}{x} P_{\mi{L}}^{~ x} (1 - P_{\mi{L}})^{~ n-x} & = & \alpha /2 \\[0.1in] \sum _{x=0}^{n_1} \binom {n}{x} P_{\mi{U}}^{~ x} (1 - P_{\mi{U}})^{~ n-x} & = & \alpha /2 \end{eqnarray*}$

$n_1 = 0$ の場合、下側信頼限界がゼロになり、 $n_1 = n$ の場合、上側信頼限界が1になります。

FREQプロシジャは、F分布を使用して、正確な(Clopper-Pearson)信頼限界を次のように計算します。

$P_{\mi{L}} = \left( 1 + \frac{n - n_1 + 1}{n_1 ~ F(~ \alpha /2, ~ 2 n_1,~ 2(n - n_1 + 1) ~ )} \right)^{-1}$

$P_{\mi{U}} = \left( 1 + \frac{n - n_1}{(n_1 + 1) ~ F(~ 1-\alpha /2, ~ 2(n_1 + 1), ~ 2(n - n_1) ~ )} \right)^{-1}$

ここで、 $F(\alpha /2, b, c)$ は、自由度bおよびc を持つF分布の $\alpha /2$ 番目のパーセント点です。この式の導出についてはLeemis and Trivedi (1996)を参照してください。正確な二項比率の信頼限界の詳細については、Collett (1991)も参照してください。

これは離散的な問題であるため、正確な(Clopper-Pearson)信頼区間の信頼係数(包含確率) は、厳密には $(1-\alpha )$ ではなく最小で $(1-\alpha )$ となります。このため、この信頼区間は保守的となります。標本サイズが大きくない場合、実際の包含確率はターゲット値よりも非常に大きくなります。これらの信頼限界の性能に関する詳細は、Agresti and Coull (1998)、Brown, Cai, and DasGupta (2001)、およびLeemis and Trivedi (1996)を参照してください。

Agresti-Coull信頼限界

CL=AGRESTICOULL binomial-optionを指定すると、FREQプロシジャは二項比率のAgresti-Coull信頼限界を次のように計算します。

$\tilde{p} ~ \pm ~ ( ~ z_{\alpha /2} \times \sqrt { \tilde{p} ~ (1-\tilde{p}) ~ / ~ \tilde{n} } ~ )$

ここで、

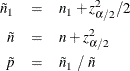
$\begin{eqnarray*} \tilde{n}_1 & = & n_1 + z_{\alpha /2}^2/2 \\ \tilde{n} & = & n + z_{\alpha /2}^2 \\ \tilde{p} & = & \tilde{n}_1 ~ / ~ \tilde{n} \end{eqnarray*}$

Agresti-Coull信頼区間は、標準Wald区間と同じ基盤を持ちますが、前者は $\hat{p}$ の代わりに $\tilde{p}$ を使用します。 $\alpha =0.05$ である場合、 $z_{\alpha /2}$ の値は2に近くなるため、この区間は、Agresti and Coull (1998)が提唱した“成功2と失敗2”を追加するように調整されたWald区間になります。

Blaker信頼限界

CL=BLAKER binomial-optionを指定すると、FREQプロシジャは二項比率のBlaker信頼限界を計算します。これは、両側の正確なBlaker検定を反転することにより構成されます(Blaker, 2000)。 $100(1-\alpha )$ %のBlaker信頼区間は、検定統計量 $B(p_{\mi{0}}, n_1)$ が選択域に入る、比率 $\mathit{p_0}$ のすべての値により構成されます。

$\{ p_{\mi{0}}: B(p_{\mi{0}}, n_1) > \alpha \}$

ここで、

$B( p_{\mi{0}}, n_1 ) ~ = ~ \mr{Prob}(~ \gamma (p_{\mi{0}}, X) \leq \gamma (p_{\mi{0}}, n_1)~ |~ p_{\mi{0}}~ )$

$\gamma ( p_{\mi{0}}, n_1 ) ~ = ~ \min (~ \mr{Prob}(~ X \geq n_1~ |~ p_{\mi{0}}~ ),~ \mr{Prob}(~ X \leq n_1~ |~ p_{\mi{0}}~ )~ )$

また、Xは二項ランダム変数です。詳細は、Blaker (2000)を参照してください。

Jeffreys信頼限界

CL=JEFFREYS binomial-optionを指定すると、FREQプロシジャは二項比率のJeffreys信頼限界を次のように計算します。

$\bigl ( ~ \beta ( \alpha /2, ~ n_1 + 1/2, ~ n - n_1 + 1/2 ), ~ ~ \beta ( 1-\alpha /2, ~ n_1 + 1/2, ~ n - n_1 + 1/2 ) ~ \bigr )$

ここで、 $\beta ( \alpha , b, c)$ は、形状パラメータbおよびcを持つベータ分布の $\alpha$ 番目のパーセント点です。 $n_1 = 0$ の場合、下側信頼限界がゼロに設定され、 $n_1 = n$ の場合、上側信頼限界が1に設定されます。これは、二項比率の無情報Jeffreys事前分布に基づくEqual-tailed区間になります。詳細は、Brown, Cai, and DasGupta (2001)を参照してください。二項比率の推定のためのベータ事前分布に関する詳細は、Berger (1985)を参照してください。

尤度比信頼限界

CL=LIKELIHOODRATIO binomial-optionを指定すると、FREQプロシジャは、尤度比検定を反転することにより二項比率の尤度比信頼限界を計算します。比率が $\mathit{p_0}$ に等しい帰無仮説の尤度比検定統計量は、次のように表されます。

$L(p_{\mi{0}} ~ = ~ -2 \left( n_1 \log ( \hat{p} / p_{\mi{0}} ) ~ + ~ (n - n_1) \log ( (1-\hat{p}) / (1-p_{\mi{0}}) ) \right)$

$100(1-\alpha )$ %の尤度比信頼区間は、検定統計量 $B(p_{\mi{0}}, n_1)$ が選択域に入る、 $\mathit{p_0}$ のすべての値により構成されます。

$\{ p_{\mi{0}}: L( p_{\mi{0}} ) < \chi ^2_{1, \alpha } \}$

ここで、 $\chi ^2_{1, \alpha }$ は、自由度が1であるカイ2乗分布の100 $(1-\alpha )$ 番目のパーセント点です。FREQプロシジャは、反復計算により信頼限界を求めます。詳細は、Fleiss, Levin, and Paik (2003)、Brown, Cai, and DasGupta (2001)、Agresti (2013)、Newcombe (1998b)を参照してください。

ロジット信頼限界

CL=LOGIT binomial-optionを指定すると、FREQプロシジャは二項比率のロジット信頼限界を計算します。これはロジット変換 $Y = \log ( \hat{p} / (1 - \hat{p}) )$ に基づいています。Yの近似信頼限界は、次のように計算されます。

$Y_{\mi{L}} ~ = ~ \log ( \hat{p}/(1-\hat{p}) ) ~ - ~ z_{\alpha /2} \sqrt { n / (n_1 (n-n_1)) }$

$Y_{\mi{U}} ~ = ~ \log ( \hat{p}/(1-\hat{p}) ) ~ + ~ z_{\alpha /2} \sqrt { n / (n_1 (n-n_1)) }$

次のように、Yの信頼限界を反転して、二項比率pの $100(1-\alpha )$ %ロジット信頼限界 $P_{\mi{L}}$ および $P_{\mi{U}}$ を求めます。

$P_{\mi{L}} ~ = ~ \exp ( Y_{\mi{L}} / ( 1 + \exp ( Y_{\mi{L}} ) )$

$P_{\mi{U}} ~ = ~ \exp ( Y_{\mi{U}} / ( 1 + \exp ( Y_{\mi{U}} ) )$

詳細は、Brown, Cai, and DasGupta (2001)およびKorn and Graubard (1998)を参照してください。

Mid-p信頼限界

CL=MIDP binomial-optionを指定すると、FREQプロシジャは、mid-p裾領域を含む2つの片側二項検定を反転することにより二項比率の正確なmid-p信頼限界を計算します。mid-p手法では、観測された度数の確率が、Clopper-Pearson合計におけるその確率の半分に置き換えられます。詳細は、正確な(Clopper-Pearson)信頼限界のセクションを参照してください。正確なmid-p信頼限界 $P_{\mi{L}}$ および $P_{\mi{U}}$ は、次の方程式の解です。

$\begin{eqnarray*} \sum _{x=n_1+1}^{n} \binom {n}{x} P_{\mi{L}}^{~ x} (1 - P_{\mi{L}})^{~ n-x} ~ + ~ \frac{1}{2} \binom {n}{n_1} P_{\mi{L}}^{~ n_1} (1 - P_{\mi{L}})^{~ n-n_1} & = & \alpha /2 \\[0.1in] \sum _{x=0}^{n_1-1} \binom {n}{x} P_{\mi{U}}^{~ x} (1 - P_{\mi{U}})^{~ n-x} ~ + ~ \frac{1}{2} \binom {n}{n_1} P_{\mi{U}}^{~ n_1} (1 - P_{\mi{U}})^{~ n-n_1} & = & \alpha /2 \end{eqnarray*}$

詳細は、Agresti and Gottard (2007)、Agresti (2013)、Newcombe (1998b)、Brown, Cai, and DasGupta (2001)を参照してください。

Wilson (スコア)信頼限界

CL=WILSON binomial-optionを指定すると、FREQプロシジャは二項比率のWilson信頼限界を計算します。これはスコア信頼限界とも呼ばれます(Wilson, 1927)。この信頼限界は、帰無仮説の分散比を使用した正規検定(スコア検定)の反転に基づいています。 Wilson信頼限界は次の根になります。

$| p - \hat{p} | = z_{\alpha /2} \sqrt { p (1-p)/n }$

これは次のように計算されます。

$\left( \hat{p} ~ + ~ z_{\alpha /2}^2/2n ~ \pm ~ z_{\alpha /2} \sqrt { \left( \hat{p} (1-\hat{p}) + z_{\alpha /2}^2 / 4n \right) / n } ~ \right) ~ / ~ \left( 1 + z_{\alpha /2}^2 / n \right)$

CL=WILSON(CORRECT)またはCORRECT binomial-optionを指定すると、FREQ プロシジャは連続性補正Wilson信頼限界を計算します。これは、次の根として計算されます。

$| p - \hat{p} | - 1/2n = z_{\alpha /2} \sqrt { p (1-p)/n }$

Wilson区間は、Wald区間や正確な(Clopper-Pearson)区間よりも高い性能を持つことが証明されています。詳細は、Agresti and Coull (1998)、Brown, Cai, and DasGupta (2001)、およびNewcombe (1998b)を参照してください。

二項検定

BINOMIALオプションを指定すると、デフォルトで、二項比率の漸近等価性の検定が実施されます。また、binomial-optionsを指定することでも、二項比率の非劣性、優越性、同等性の検定を要求できます。EXACTステートメントでBINOMIALオプションを指定すると、FREQプロシジャは、binomial-optionsで要求された検定の正確なp値も計算します。

等価性の検定

FREQプロシジャは、二項比率が $p_0$ に等しいという仮説の漸近検定を計算します。ここで、 $p_0$ の値を指定するには、P=binomial-optionを使用します。P=にヌル値以外を指定すると、FREQプロシジャはデフォルト $p_0 = 0.5$ を使用します。二項検定は次のように計算されます。

$z = ( \hat{p} - p_0 ) / \mr{se}$

デフォルトでは、標準誤差は、帰無仮説の比率に基づいて次のように計算されます。

$\mr{se} = \sqrt { p_0 ( 1 - p_0 ) / n}$

VAR=SAMPLE binomial-optionを指定すると、次のように、標本比率から標準誤差が計算されます。

$\mr{se} = \sqrt { \hat{p} ( 1 - \hat{p} ) / n }$

CORRECT binomial-optionを指定すると、FREQプロシジャは、正規近似と離散的な二項分布間の差異を調整するために、漸近検定統計量に連続性補正を含めます。詳細は、Fleiss, Levin, and Paik (2003)を参照してください。 $(1/2n)$ の連続性補正は、 $(\hat{p} - p_0)$ が正数である場合、検定統計量の分子から差し引かれます。それ以外の場合、連続性補正は同分子に追加されます。

FREQプロシジャは、この検定の片側および両側のp値を計算します。検定統計量zがゼロ(帰無仮説の下でのその期待値)より大きい場合、FREQプロシジャは、右側p値を計算します。これは、帰無仮説の下で統計量の大きい値が発生する確率になります。小さい右側p値は、比率の真の値が $p_0$ より大きいという対立仮説を支持します。この検定統計量がゼロ以下である場合、FREQプロシジャは、左側p値を計算します。これは、帰無仮説の下で統計量の小さな値が発生する確率になります。小さな左側p値は、比率の真の値が $p_0$ より小さいという対立仮説を支持します。片側のp値 $P_1$ は、次のように計算されます。

$\begin{equation*} P_1 = \begin{cases} \mr{Prob} (Z > z) \quad \mr{if} \hspace{.1in} z > 0 \\ \mr{Prob} (Z < z) \quad \mr{if} \hspace{.1in} z \leq 0 \\ \end{cases}\end{equation*}$

ここで、Zは標準正規分布に従います。両側のp値は、 $P_2 = 2 \times P_1$ として計算されます。

EXACT ステートメントでBINOMIALオプションを指定すると、FREQプロシジャは、帰無仮説 $H_0\colon p = p_0$ の正確検定も計算します。正確検定を計算する場合、FREQプロシジャは次のような二項確率関数を使用します。

$\mr{Prob} (X = x ~ | ~ p_0 ) = \binom {n}{x} p_0^{~ x} ~ (1-p_0)^{~ (n-x)} \hspace{.2in} \mr{for} \hspace{.1in} x = 0,1,2, \ldots ,n$

ここで、変数Xはパラメータnおよび $p_0$ を持つ二項分布に従います。左側p値 $\mr {Prob} (X \leq n_1)$ を計算する場合、FREQプロシジャは、xの二項確率を、ゼロから $n_1$ まで合計します。右側p値 $\mr {Prob} (X \geq n_1)$ を計算する場合、FREQプロシジャは、xの二項確率を $n_1$ からnまで合計します。正確な片側p値は、次に示すように、右側および左側p値の最小値となります。

$P_{1} = \min ~ ( ~ \mr{Prob}(X \leq n_1 ~ | ~ p_0 ), ~ \mr{Prob}(X \geq n_1 ~ | ~ p_0 ) ~ )$

両側のp値は、 $P_{2} = 2 \times P_{1}$ として計算されます。

非劣性の検定

NONINF binomial-optionを指定すると、FREQプロシジャは二項比率の非劣性の検定を実施します。非劣性の検定の帰無仮説は、次のようになります。

$H_0\colon p - p_0 \leq -\delta$

対立仮説は次のようになります。

$H_ a\colon p - p_0 > -\delta$

ここで、 $\delta$ は非劣性のマージンであり、 $p_0$ は帰無仮説の比率です。帰無仮説の棄却は、二項比率がヌル値に対して劣性でないことを示します。詳細は、Chow, Shao, and Wang (2003)を参照してください。

$\delta$ の値を指定するには、MARGIN= binomial-optionを使用します。 $p_0$ を指定するには、P= binomial-optionを使用します。デフォルトでは、 $\delta = 0.2$ および $p_0 = 0.5$ になります。

FREQプロシジャは、非劣性の漸近Wald検定も実施します。検定統計量は次のように計算されます。

$z = ( \hat{p} - p_0^\ast ) ~ / ~ \mr{se}$

ここで、 $p_0^\ast$ は非劣性の限界であり、次の式が成り立ちます。

$p_0^\ast = p_0 - \delta$

デフォルトでは、標準誤差は、標本比率から次のように計算されます。

$\mr{se} = \sqrt { \hat{p} (1 - \hat{p}) / n}$

VAR=NULL binomial-optionを指定すると、標準誤差は非劣性の限界(帰無仮説の比率とマージンにより決定されるもの)に基づいて次のように計算されます。

$\mr{se} = \sqrt { p_0^\ast (1 - p_0^\ast ) / n}$

CORRECT binomial-optionを指定すると、FREQプロシジャは漸近検定統計量zに連続性補正を含めます。 $(1/2n)$ の連続性補正は、 $(\hat{p} - p_0^\ast )$ が正数である場合、検定統計量の分子から差し引かれます。それ以外の場合、連続性補正は同分子に追加されます。

非劣性の検定のp値は次のようになります。

$P_ z = \mr{Prob} ( Z > z )$

ここで、Zは標準正規分布を持ちます。

非劣性の分析の一部として、FREQプロシジャは、二項比率の漸近Wald信頼限界を計算します。これらの信頼限界は、Wald信頼限界のセクションで示した方法で計算されますが、非劣性の検定統計量zの場合と同じ標準誤差(VAR=NULLまたはVAR=SAMPLE)を使用します。信頼係数は $100(1-2\alpha )$ %です(Schuirmann, 1999)。ALPHA=オプションを省略すると、非劣性の信頼限界はデフォルトで90%の信頼限界となります。この信頼限界を非劣性の限界 $p_0^\ast = p_0 - \delta$ と比較できます。

EXACTステートメントでBINOMIALオプションを指定すると、FREQプロシジャは、二項比率の正確な非劣性の検定も計算します。正確なp値は、パラメータ $p_0^\ast$ およびn値を持つ二項確率関数を使用して次のように計算されます。

$P_ x = \sum _{k=n_1}^{k=n} \binom {n}{k} (p_0^\ast )^{~ k} ~ (1-p_0^\ast )^{~ (n-k)}$

詳細については、Chow, Shao, and Wang (2003, p. 116)を参照してください。正確な二項統計量を要求する場合、FREQは、同等性の分析の表示の中に、二項比率の正確な(Clopper-Pearson)信頼限界も含めます。詳細は、正確な(Clopper-Pearson)信頼限界のセクションを参照してください。

優越性の検定

SUP binomial-optionを指定すると、FREQプロシジャは、二項比率の優越性の検定を実施します。優越性の検定の帰無仮説は、次のように表されます。

$H_0\colon p - p_0 \leq \delta$

対立仮説は次のようになります。

$H_ a\colon p - p_0 > \delta$

ここで、 $\delta$ 優越性のマージンであり、 $p_0$ は帰無仮説の比率です。帰無仮説の棄却は、二項比率がヌル値に対して優越していることを示します。 $\delta$ の値を指定するには、MARGIN= binomial-optionを使用します。 $p_0$ の値を指定するには、P= binomial-optionを使用します。デフォルトでは、 $\delta = 0.2$ および $p_0 = 0.5$ になります。

優越性の分析は非劣性の分析と同じですが、帰無仮説で正のマージン値 $\delta$ を使用するところが違います。優越性の限界は $p_0 + \delta$ に等しくなります。優越性の計算は非劣性の検定のセクションに示されている方法に従いますが、– $\delta$ の代わりに $\delta$ を使用します。詳細は、Chow, Shao, and Wang (2003)を参照してください。

同等性検定

EQUIV binomial-optionを指定すると、FREQプロシジャは、二項比率の同等性の検定を実施します。同等性の検定の帰無仮説は次のようになります。

$H_0\colon p - p_0 \leq \delta _{\mi{L}} \hspace{.15in} \mr{or} \hspace{.15in} p - p_0 \geq \delta _{\mi{U}}$

対立仮説は次のようになります。

$H_ a\colon \delta _{\mi{L}} < p - p_0 < \delta _{\mi{U}}$

ここで、 $\delta _{\mi {L}}$ は下限マージン、 $\delta _{\mi {U}}$ は上限マージン、 $p_0$ は帰無仮説の比率です。帰無仮説の棄却は、二項比率がヌル値に対して同等であることを示します。詳細は、Chow, Shao, and Wang (2003)を参照してください。

マージン値 $\delta _ L$ および $\delta _ U$ を指定するには、MARGIN= binomial-optionを使用します。MARGIN=を指定しない場合、FREQプロシジャはデフォルトの下限マージンおよび上限マージンとして、それぞれ–0.2および0.2を使用します。単一のマージン値 $\delta$ を指定すると、FREQプロシジャは下限マージンおよび上限マージンとして、それぞれ– $\delta$ および $\delta$ を使用します。帰無仮説の比率 $p_0$ を指定するには、P= binomial-optionを使用します。デフォルトでは、 $p_0 = 0.5$ になります。

FREQプロシジャは、同等性の分析で、2つの片側検定(TOST)を計算します (Schuirmann, 1987)。TOST手法には、下限マージンの右側検定と、上限マージンの左側検定が含まれます。全体的なp値は、下側および上側の検定における2つのp値のうちの大きい方になります。

下限マージンの場合、漸近Wald検定統計量は次のように計算されます。

$z_{\mi{L}} = ( \hat{p} - p_{\mi{L}}^\ast ) ~ / ~ \mr{se}$

ここで、下側同等性限界は次のようになります。

$p_{\mi{L}}^\ast = p_0 + \delta _{\mi{L}}$

デフォルトでは、標準誤差は、標本比率から次のように計算されます。

$\mr{se} = \sqrt { \hat{p} (1 - \hat{p}) / n}$

VAR=NULL binomial-optionを指定すると、標準誤差は下側同等性限界(帰無仮説の比率と下限マージンにより決定されるもの)に基づいて次のように計算されます。

$\mr{se} = \sqrt { p_{\mi{L}}^\ast (1 - p_{\mi{L}}^\ast ) / n}$

CORRECT binomial-optionを指定すると、FREQプロシジャは漸近検定統計量 $z_{\mi {L}}$ に連続性補正を含めます。 $(1/2n)$ の連続性補正は、検定統計量 $(\hat{p} - p_{\mi {L}}^\ast )$ の分子が正数である場合、同分子から差し引かれます。それ以外の場合、連続性補正は同分子に追加されます。

下限マージン検定のp値は次のようになります。

$P_{z,\mi{L}} = \mr{Prob} ( Z > z_{\mi{L}} )$

上限マージンの漸近検定も同様に計算されます。Wald検定統計量は次のように表されます。

$z_{\mi{U}} = ( \hat{p} - p_{\mi{U}}^\ast ) ~ / ~ \mr{se}$

ここで、同等性の上限は次のようになります。

$p_{\mi{U}}^\ast = p_0 + \delta _{\mi{U}}$

デフォルトでは、標準誤差は、標本母集団から計算されます。VAR=NULL binomial-optionを指定すると、標準誤差は上側同等性限界に基づいて次のように計算されます。

$\mr{se} = \sqrt { p_{\mi{U}}^\ast (1 - p_{\mi{U}}^\ast ) / n}$

CORRECT binomial-optionを指定すると、FREQプロシジャは漸近検定統計量 $z_{\mi {U}}$ に $(1/2n)$ の連続性補正を含めます。

上限マージン検定のp値は次のようになります。

$P_{z,\mi{U}} = \mr{Prob} ( Z < z_{\mi{U}} )$

2つの片側検定(TOST)に基づく場合、同等性の検定の全体的なp値は、下限および上限マージン検定のp値以上になります。これは次のように表されます。

$P_ z = \max ( P_{z,\mi{L}} ~ , ~ P_{z,\mi{U}} )$

同等性の分析の一部として、FREQプロシジャは、二項比率の漸近Wald信頼限界を計算します。これらの信頼限界は、Wald信頼限界のセクションで示した方法で計算されますが、同等性の検定統計量の場合と同じ標準誤差(VAR=NULLまたはVAR=SAMPLE)を使用し、かつ $100(1-2\alpha )$ %の信頼係数を持ちます(Schuirmann, 1999)。ALPHA=を省略すると、これらはデフォルトで90%の信頼限界になります。VAR=NULLを指定すると、下限および上限マージン検定で、それぞれ帰無仮説の比率と対応する(下限または上限)マージンに基づいて、別々の標準誤差が計算されます。これらの信頼限界は、これらの2つの標準誤差の最大値を使用して計算されます。信頼限界を同等性の限界 $( p_0 + \delta _{\mi {L}}, ~ p_0 + \delta _{\mi {U}} )$ と比較できます。

EXACTステートメントでBINOMIALオプションを指定すると、FREQプロシジャは、2つの片側正確検定(TOST)を使用した正確な同等性の検定も実施します。同プロシジャは、非劣性の検定のセクションに示されている二項確率関数を使用して上限および下限マージンの正確検定を計算します。同等性の検定の全体的な正確なp値は、下限および上限マージンの正確検定のp値において大きい方になります。正確検定を要求する場合、FREQプロシジャは、同等性の分析の表示に正確な(Clopper-Pearson)信頼限界も含めます。信頼係数は $100(1-2\alpha )$ %です(Schuirmann, 1999)。詳細は、正確な(Clopper-Pearson)信頼限界のセクションを参照してください。