FREQプロシジャ
連関性の統計量
TABLESステートメントでMEASURESオプションを指定すると、FREQプロシジャは、分割表の行変数と列変数の間の連関性を記述する複数の統計量を計算します。行変数Xが増加するにつれ列変数Yが増加する傾向にあるかどうかを検討する順序関連性の指標としては、ガンマ、Kendallのtau- 、Stuartのtau-
、Stuartのtau- 、Somersの
、Somersの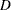 があります。これらの統計量は順序変数に適しており、これらの統計量によりオブザベーションのペアを 一致または不一致として分類できます。オブザベーションでXの値が大きいほどYの値も大きくなる場合、そのペアは一致となります。オブザベーションでXの値が大きいほどYの値が小さくなる場合、そのペアは不一致となります。関連性の指標の詳細は、Agresti (2007)および各統計量の説明で示されているリファレンスを参照してください。
があります。これらの統計量は順序変数に適しており、これらの統計量によりオブザベーションのペアを 一致または不一致として分類できます。オブザベーションでXの値が大きいほどYの値も大きくなる場合、そのペアは一致となります。オブザベーションでXの値が大きいほどYの値が小さくなる場合、そのペアは不一致となります。関連性の指標の詳細は、Agresti (2007)および各統計量の説明で示されているリファレンスを参照してください。
Pearsonの相関係数とSpearmanの順位相関係数も、順序変数に適しています。Pearsonの相関は、行変数と列変数間のリニアな連関性の強度を記述するものであり、TABLESステートメントのSCORES=で指定された行変数と列変数を使用して計算されます。Spearmanの相関は、ランクスコアを使用して計算されます。Polychoricの相関(PLCORRオプションにより要求される)も順序変数を必要とし、変数が基礎的な2変量正規分布に従うことを仮定します。関連性の指標のうち、非対象ラムダ、対称ラムダ、不確定性係数は順序変数を必要としないため、名義変数に適しています。
FREQプロシジャは、これ以降の各セクションで示す公式に従って統計量の推定値を計算します。 各統計量に関して、FREQプロシジャは、漸近標準誤差( )を計算します。これは、以降のセクションでは
)を計算します。これは、以降のセクションでは で表される漸近分散の平方根になります。
で表される漸近分散の平方根になります。
信頼区間
TABLESステートメントでCLオプションを指定すると、FREQプロシジャは、すべてのMEASURES統計量の漸近信頼限界を計算します。信頼限界はALPHA=オプションの値に従って決定されます。この値はデフォルトで0.05であり、信頼限界は95%になります。
信頼限界は次のように計算されます。
 |
ここで、 は統計量の推定値、
は統計量の推定値、 は標準正規分布の
は標準正規分布の 番目のパーセント点、
番目のパーセント点、 は推定値の漸近標準誤差です。
は推定値の漸近標準誤差です。
漸近検定
TESTステートメントで統計量を指定すると、FREQプロシジャは、その統計量がゼロに等しいという帰無仮説に関する漸近的な検定を計算します。漸近検定は、ガンマ、Kendallのtau- 、Stuartのtau-
、Stuartのtau- 、Somersの
、Somersの 、Somersの
、Somersの 、Pearsonの相関係数、Spearmanの順位相関係数のような関連性の指標に関して利用できます。漸近検定を計算する場合、FREQプロシジャは、標準化された検定統計量
、Pearsonの相関係数、Spearmanの順位相関係数のような関連性の指標に関して利用できます。漸近検定を計算する場合、FREQプロシジャは、標準化された検定統計量 を使用します。これは、帰無仮説の下で漸近標準正規分布に従います。検定統計量は次のように計算されます。
を使用します。これは、帰無仮説の下で漸近標準正規分布に従います。検定統計量は次のように計算されます。
 |
ここで、 は統計量の推定値、
は統計量の推定値、 は帰無仮説の下での推定値の分散です。個々の関連性の指標を計算する
は帰無仮説の下での推定値の分散です。個々の関連性の指標を計算する 公式は、各統計量について説明したセクションで示します。
公式は、各統計量について説明したセクションで示します。
次に示す統計量では、 の
の に対する比が同じになります。これには、ガンマ、Kendallのtau-
に対する比が同じになります。これには、ガンマ、Kendallのtau- 、Stuartのtau-
、Stuartのtau- 、Somersの
、Somersの 、Somersの
、Somersの が含まれます。このため、これらの統計量に関する検定は同じになります。たとえば、
が含まれます。このため、これらの統計量に関する検定は同じになります。たとえば、 の検定の
の検定の 値は、
値は、 の検定の
の検定の 値に等しくなります。
値に等しくなります。
FREQプロシジャは、これらの各検定の片側および両側の 値を計算します。検定統計量
値を計算します。検定統計量 がその帰無仮説の期待値ゼロよりも大きい場合、FREQプロシジャは右側
がその帰無仮説の期待値ゼロよりも大きい場合、FREQプロシジャは右側 値を表示します。これは、帰無仮説の下で統計量の大きな値が発生する確率になります。小さい右側
値を表示します。これは、帰無仮説の下で統計量の大きな値が発生する確率になります。小さい右側 値は、測定値の真の値がゼロより大きいという対立仮説を支持します。この検定統計量がゼロ以下である場合、FREQプロシジャは、左側
値は、測定値の真の値がゼロより大きいという対立仮説を支持します。この検定統計量がゼロ以下である場合、FREQプロシジャは、左側 値を表示します。これは、帰無仮説の下で統計量の小さな値が発生する確率になります。小さな左側
値を表示します。これは、帰無仮説の下で統計量の小さな値が発生する確率になります。小さな左側 値は、測定値の真の値がゼロより小さいという対立仮説を支持します。片側の
値は、測定値の真の値がゼロより小さいという対立仮説を支持します。片側の 値
値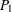 は次のように計算されます。
は次のように計算されます。
 |
ここで、 は標準正規分布を持ちます。両側のp値
は標準正規分布を持ちます。両側のp値 は次のように計算されます。
は次のように計算されます。
 |
正確検定
正確検定は、Kendallのtau- 、Stuartのtau-
、Stuartのtau- 、Somersの
、Somersの および
および 、Pearsonの相関係数、Spearmanの順位相関係数のような関連性の指標に関して利用できます。EXACTステートメントで関連性の指標の正確検定を要求すると、FREQプロシジャは、統計量がゼロに等しいという仮説に関する正確検定を計算します。詳細は、正確な統計量のセクションを参照してください。
、Pearsonの相関係数、Spearmanの順位相関係数のような関連性の指標に関して利用できます。EXACTステートメントで関連性の指標の正確検定を要求すると、FREQプロシジャは、統計量がゼロに等しいという仮説に関する正確検定を計算します。詳細は、正確な統計量のセクションを参照してください。
ガンマ
ガンマ(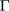 )統計量は、2つのオブザベーション間の一致および不一致の数にのみ基づきます。これはタイのペア(すなわち、
)統計量は、2つのオブザベーション間の一致および不一致の数にのみ基づきます。これはタイのペア(すなわち、 の値が等しいか、または
の値が等しいか、または の値が等しいオブザベーションのペア)を無視します。ガンマは、両変数が順序尺度である場合にのみ適用できます。ガンマの範囲は、
の値が等しいオブザベーションのペア)を無視します。ガンマは、両変数が順序尺度である場合にのみ適用できます。ガンマの範囲は、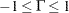 になります。行変数と列変数が独立である場合、ガンマはゼロに近づく傾向があります。ガンマは次のように計算されます。
になります。行変数と列変数が独立である場合、ガンマはゼロに近づく傾向があります。ガンマは次のように計算されます。
 |
漸近分散は
 |
 表の場合、ガンマはYuleの
表の場合、ガンマはYuleの に等しくなります。詳細は、Goodman and Kruskal (1979)およびAgresti (2002)を参照してください。
に等しくなります。詳細は、Goodman and Kruskal (1979)およびAgresti (2002)を参照してください。
ガンマがゼロに等しい帰無仮説の下での分散は次のように計算されます。
 |
詳細は、Brown and Benedetti (1977)を参照してください。
KendallのTau-b
Kendallのtau- (
( )はガンマに似ていますが、tau-
)はガンマに似ていますが、tau- はタイに関する修正を使用する点が異なります。Tau-
はタイに関する修正を使用する点が異なります。Tau- は、両変数が順序尺度である場合にのみ適用できます。Tau-
は、両変数が順序尺度である場合にのみ適用できます。Tau- の範囲は
の範囲は になります。Kendallのtau-
になります。Kendallのtau- は次のように計算されます。
は次のように計算されます。
 |
漸近分散は次のように計算されます。
 |
説明
 |
 |
 |
|||
 |
 |
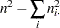 |
|||
 |
 |
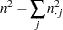 |
|||
 |
 |
 |
|||
 |
 |
 |
詳細は、Kendall (1955)を参照してください。
tau- がゼロに等しい帰無仮説の下での分散は次のように計算されます。
がゼロに等しい帰無仮説の下での分散は次のように計算されます。
 |
詳細は、Brown and Benedetti (1977)を参照してください。
FREQプロシジャは、Kendallのtau- に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでKENTBオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでKENTBオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
Stuartのtau-c
Stuartのtau- (
( )は、タイの修正に加えて、表サイズを調整します。Tau-
)は、タイの修正に加えて、表サイズを調整します。Tau- は、両変数が順序尺度である場合にのみ適用できます。Tau-
は、両変数が順序尺度である場合にのみ適用できます。Tau- の範囲は
の範囲は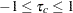 になります。Stuartのtau-
になります。Stuartのtau- は次のように計算されます。
は次のように計算されます。
 |
漸近分散は
 |
ここで、 および
および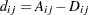 です。tau-
です。tau- がゼロに等しい帰無仮説の下での分散は、漸近分散
がゼロに等しい帰無仮説の下での分散は、漸近分散 と同じになります。
と同じになります。
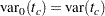 |
詳細は、Brown and Benedetti (1977)を参照してください。
FREQプロシジャは、Stuartのtau- に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでSTUTCオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでSTUTCオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
SomersのD
Somersの およびSomersの
およびSomersの はtau-
はtau- の非対称的な変形です。
の非対称的な変形です。 は、行変数Xを独立変数として、列変数Yを従属変数として見なすことを意味します。同様に、
は、行変数Xを独立変数として、列変数Yを従属変数として見なすことを意味します。同様に、 は、列変数Yを独立変数として、行変数Xを従属変数として見なすことを示します。Somersの
は、列変数Yを独立変数として、行変数Xを従属変数として見なすことを示します。Somersの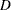 がtau-
がtau- と異なる点は、前者は独立変数に関してタイであるペアに対してのみ修正を適用することにあります。Somersの
と異なる点は、前者は独立変数に関してタイであるペアに対してのみ修正を適用することにあります。Somersの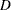 は、両変数が順序尺度である場合にのみ適用できます。Somersの
は、両変数が順序尺度である場合にのみ適用できます。Somersの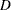 の範囲は
の範囲は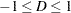 になります。Somersの
になります。Somersの は次のように計算されます。
は次のように計算されます。
 |
およびその漸近分散は
 |
ここで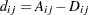 および
および
 |
詳細は、Somers (1962)、Goodman and Kruskal (1979)、およびLiebetrau (1983)を参照してください。
 がゼロに等しい帰無仮説の下での分散は次のように計算されます。
がゼロに等しい帰無仮説の下での分散は次のように計算されます。
 |
詳細は、Brown and Benedetti (1977)を参照してください。
Somersの の公式は、添え字を交換することにより導びかれます。
の公式は、添え字を交換することにより導びかれます。
FREQプロシジャは、Somersの およびSomersの
およびSomersの に関する正確検定も提供します。これらの正確検定を要求するには、EXACTステートメントでそれぞれSMDCRオプションおよびSMDCRオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
に関する正確検定も提供します。これらの正確検定を要求するには、EXACTステートメントでそれぞれSMDCRオプションおよびSMDCRオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
Pearson相関係数
Pearsonの相関係数(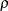 )は、SCORES=オプションに指定されたスコアを使用して計算されます。この測定は、両変数が順序尺度である場合にのみ適用できます。Pearson相関係数の範囲は、
)は、SCORES=オプションに指定されたスコアを使用して計算されます。この測定は、両変数が順序尺度である場合にのみ適用できます。Pearson相関係数の範囲は、 になります。Pearsonの相関係数は次のように計算されます。
になります。Pearsonの相関係数は次のように計算されます。
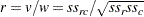 |
およびその漸近分散は
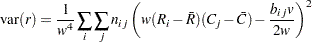 |
ここで、 および
および はそれぞれ行スコアおよび列スコアであり、次の式が成り立ちます。
はそれぞれ行スコアおよび列スコアであり、次の式が成り立ちます。
 |
 |
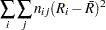 |
|||
 |
 |
 |
|||
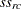 |
 |
 |
 |
 |
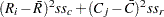 |
|||
 |
 |
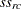 |
|||
 |
 |
 |
詳細は、Snedecor and Cochran (1989)を参照してください。
TABLESステートメントのSCORES=オプションは、Pearson相関係数(およびその他のスコアに基づく統計量)の計算に使用される行スコアおよび列スコアのタイプを指定します。デフォルトはSCORES=TABLEです。利用可能なスコアタイプとそれらの計算方法についての詳細は、スコアのセクションを参照してください。
相関がゼロに等しい帰無仮説のもとでの分散は次のように計算されます。
 |
この分散式は、分割表のフレームワークにおける多項標本抽出で導出されるものであり、両変数が連続でありかつ正規分布に従うという仮定の下で導かれる形式とは異なっています。詳細は、Brown and Benedetti (1977)を参照してください。
FREQプロシジャは、Pearsonの相関係数に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでPCORRオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
Spearmanの順位相関係数
Spearmanの相関係数( )を計算するには、スコアのセクションで定義されているランクスコアを使用します。この測定は、両変数が順序尺度である場合にのみ適用できます。Spearman相関係数の範囲は、
)を計算するには、スコアのセクションで定義されているランクスコアを使用します。この測定は、両変数が順序尺度である場合にのみ適用できます。Spearman相関係数の範囲は、 になります。Spearmanの相関係数は次のように計算されます。
になります。Spearmanの相関係数は次のように計算されます。
 |
およびその漸近分散は
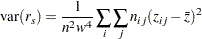 |
ここで、 および
および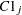 はそれぞれ行および列のランクスコアであり、次の式が成り立ちます。
はそれぞれ行および列のランクスコアであり、次の式が成り立ちます。
 |
 |
 |
|||
 |
 |
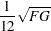 |
|||
 |
 |
 |
|||
 |
 |
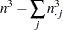 |
 |
 |
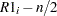 |
|||
 |
 |
 |
|||
 |
 |
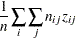 |
|||
 |
 |
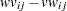 |
|||
 |
 |
 |
|||
 |
 |
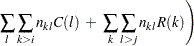 |
|||
 |
 |
 |
詳細は、Snedecor and Cochran (1989)を参照してください。
相関がゼロに等しい帰無仮説のもとでの分散は次のように計算されます。
 |
説明
 |
この漸近分散は、分割表のフレームワークにおける多項標本抽出で導出されるものであり、両変数が連続でありかつ正規分布に従うという仮定の下で導かれる形式とは異なっています。詳細は、Brown and Benedetti (1977)を参照してください。
FREQプロシジャは、Spearmanの相関係数に関する正確検定も提供しています。この検定を要求するには、EXACTステートメントでSCORRオプションを指定します。詳細は、正確な統計量のセクションを参照してください。
多分相関係数
TABLESステートメントでPLCORRオプションを指定すると、FREQプロシジャはポリコリック相関を計算します。この連関性の指標は、度数表の順序カテゴリ変数が2変量正規分布に従うという仮定に基づいています。 表の場合、ポリコリック相関は四分相関とも呼ばれます。ポリコリック相関の概要については、Drasgow (1986)を参照してください。ポリコリック相関は、正規変数間における積率相関の最尤推定値であり、観測された表の度数からしきい値を推定します。ポリコリック相関の範囲は、–1~1になります。Olsson (1979)は、この推定値に関する尤度方程式と漸近共分散行列を提供しています。
表の場合、ポリコリック相関は四分相関とも呼ばれます。ポリコリック相関の概要については、Drasgow (1986)を参照してください。ポリコリック相関は、正規変数間における積率相関の最尤推定値であり、観測された表の度数からしきい値を推定します。ポリコリック相関の範囲は、–1~1になります。Olsson (1979)は、この推定値に関する尤度方程式と漸近共分散行列を提供しています。
ポリコリック相関を計算する場合、FREQプロシジャは、Pearson相関係数を初期近似として使用するNewton-Raphsonアルゴリズムにより尤度方程式を繰り返し解きます。この反復計算は、収束測定値が収束基準を下まわった場合、または最大反復数に達した場合に停止します。CONVERGE=オプションは収束基準を指定します。デフォルト値は0.0001です。MAXITER=オプションは最大反復数を指定します。デフォルト値は20です。
非対称ラムダ
非対称ラムダ は、行変数Xに関する知識を与えられた場合の列変数Yの予測における推定的な改善として解釈されます。非対称ラムダの範囲は、
は、行変数Xに関する知識を与えられた場合の列変数Yの予測における推定的な改善として解釈されます。非対称ラムダの範囲は、 になります。非対称ラムダ(
になります。非対称ラムダ( )は次のように計算されます。
)は次のように計算されます。
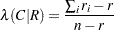 |
およびその漸近分散は
 |
説明
 |
 |
 |
|||
 |
 |
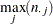 |
|||
 |
 |
 |
|||
 |
 |
 |
 および
および の値は次のように決定されます。
の値は次のように決定されます。 により
により の一意の値(
の一意の値( など)を表し、
など)を表し、 を
を の一意の値(
の一意の値(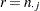 など)とします。一意性仮説により、度数または周辺度数のタイを、任意の一貫した方式で分割する必要があります。タイの場合、
など)とします。一意性仮説により、度数または周辺度数のタイを、任意の一貫した方式で分割する必要があります。タイの場合、 は
は の最小値として定義されます(
の最小値として定義されます(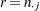 など)。
など)。
セル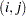 を含んでいるこれらの列で
を含んでいるこれらの列で である場合、
である場合、 は
は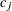 が起こると仮定される行を記録します。最初に、
が起こると仮定される行を記録します。最初に、 はすべての
はすべての で-1に設定されます。
で-1に設定されます。 で始まり、
で始まり、 となるような値
となるような値 が少なくとも1つ存在し、かつ
が少なくとも1つ存在し、かつ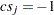 であるならば、
であるならば、 はそのような値
はそのような値 の最小値として定義され、
の最小値として定義され、 は
は に等しいものとして設定されます。それ以外の場合、
に等しいものとして設定されます。それ以外の場合、 であるならば、
であるならば、 は
は に等しいものとして定義されます。どちらの条件も真でない場合、
に等しいものとして定義されます。どちらの条件も真でない場合、 は、
は、 のような値
のような値 の最小値となります。
の最小値となります。
非対称ラムダ の公式は、添え字を交換することにより導びかれます。
の公式は、添え字を交換することにより導びかれます。
詳細は、Goodman and Kruskal (1979)を参照してください。
対称ラムダ
非指向性ラムダとは、2つの非対称ラムダ および
および の平均です。その範囲は
の平均です。その範囲は です。対称ラムダは次のように計算されます。
です。対称ラムダは次のように計算されます。
 |
その漸近分散は次のように計算されます。
 |
説明
 |
 |
 |
|||
 |
 |
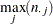 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
 および
および の定義は、前のセクションで示されています。
の定義は、前のセクションで示されています。 および
および の値は、非対称ラムダ(
の値は、非対称ラムダ( )と同様の方法で定義されます。
)と同様の方法で定義されます。
詳細は、Goodman and Kruskal (1979)を参照してください。
不確定性係数(非対称)
不確定性係数 は、行変数Xにより説明される列変数Yにおける不確定性の割合を測定するものです。その範囲は
は、行変数Xにより説明される列変数Yにおける不確定性の割合を測定するものです。その範囲は です。不確定性係数は次のように計算されます。
です。不確定性係数は次のように計算されます。
 |
およびその漸近分散は
 |
説明
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
不確定性係数 の公式は、添え字を交換することにより導びかれます。
の公式は、添え字を交換することにより導びかれます。
詳細は、Theil (1972, pp. 115–120)およびGoodman and Kruskal (1979)を参照してください。

 は、2つの非対称不確定性係数の対称版です。その範囲は
は、2つの非対称不確定性係数の対称版です。その範囲は です。不確定性係数は次のように計算されます。
です。不確定性係数は次のように計算されます。
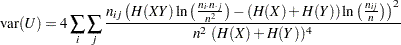
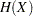 、
、 、および
、および は前のセクションで定義されています。詳細は、Goodman and Kruskal (1979)を参照してください。
は前のセクションで定義されています。詳細は、Goodman and Kruskal (1979)を参照してください。