CORRプロシジャ
例2.9 偏相関の計算
偏相関は、他の変数による影響を補正した上で2変数間の線形関係の強さを測定するものです。
次のステートメントは、変数Length3とWeightによる影響を補正した上で、変数HeightとWidth間の偏相関分析を要求します。変数Length3およびWeightのことを、分析の「影響を除外された」変数と呼び、これらはPARTIALステートメントで指定されます。
ods graphics on; title 'Fish Measurement Data'; proc corr data=fish1 plots=scatter(alpha=.20 .30); var Height Width; partial Length3 Weight3; run; ods graphics off;
出力2.9.1には、すべての変数に関する記述統計量が示されています。また、VARステートメント内に指定されている変数に関する偏分散と偏標準偏差も示されています。
出力2.9.1 記述統計量
| Fish Measurement Data |
The CORR Procedure
| 2 Partial Variables: | Length3 Weight3 |
|---|---|
| 2 Variables: | Height Width |
| Simple Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| variable | N | Mean | Std Dev | Sum | Minimum | Maximum | Partial Variance |
Partial Std Dev |
| Length3 | 34 | 38.38529 | 4.21628 | 1305 | 30.00000 | 46.50000 | ||
| Weight3 | 34 | 8.44751 | 0.97574 | 287.21524 | 6.23168 | 10.00000 | ||
| Height | 34 | 15.22057 | 1.98159 | 517.49950 | 11.52000 | 18.95700 | 0.26607 | 0.51582 |
| Width | 34 | 5.43805 | 0.72967 | 184.89370 | 4.02000 | 6.74970 | 0.07315 | 0.27047 |
PARTIALステートメントを指定すると、欠損値があるオブザベーションは分析から除外されます。出力2.9.2には、VARステートメントに指定された変数の偏相関が示されています。
出力2.9.2 Pearsonの偏相関係数
| Pearson Partial Correlation Coefficients, N = 34 Prob > |r| under H0: Partial Rho=0 |
||||||
|---|---|---|---|---|---|---|
| Height | Width | |||||
| Height |
|
|
||||
| Width |
|
|
||||
変数HeightとWidth間の偏相関は0.25692であり、元の相関0.92632よりも大幅に低くなっています(出力2.9.2を参照)。この偏相関の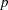 値は0.1558です。
値は0.1558です。
PLOTS=SCATTERオプションを指定すると、変数Length3およびWeightによる影響を補正した上で、変数HeightおよびWidthの残差に関する散布図を作成できます(図2.9.3を参照)。ALPHA=.20 .30サブオプションは、それぞれ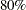 および
および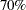 予測楕円を要求します。
予測楕円を要求します。
出力2.9.3 偏残差散布図

出力2.9.3では、Heightの標準偏差のX軸上の長さは、Y軸上のWidthの標準偏差とほぼ同じになります。長軸長が短軸長よりも大幅に大きくない場合、HeightとWidth間に弱い偏相関があることを意味します。
