CORRプロシジャ

偏相関は、2変数間の関係を他の変数による影響を補正した上で測定するものです。PARTIALステートメントで他の変数の影響を除去した後の2変数間のPearson偏相関は、これらの影響を除去する変数への回帰を引いた2変数の残差間のPearson相関に等しくなります。

を相関変数の集合、をコントロール変数の集合とします。を考慮した場合の番目と番目の変数の間の母集団Pearson編相関は、誤差と間の相関になります。ここで、

上記の式はそれぞれ、コントロール変数が与えられた場合の、変数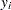およびの回帰モデルとなります。

指定のオブザベーションの例では、を考慮した場合の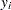と間の標本Pearson偏相関は、残差とから導かれます。ここで、

は、を考慮した場合の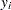および変数の回帰モデルを使用した当てはめ値です。

を考慮した場合のの偏修正済み平方和と交差積(CSSCP)は、残差の修正済み平方和と交差積になります。これらの修正済み偏差平方和積和を使用することで、偏共分散および偏相関を計算できます。

CORRプロシジャは、Cholesky分解アルゴリズムをCSSCP行列に適用することで、 偏修正済み平方和と交差積行列を導きます。偏相関の場合、 を、2変数および間の偏CSSCP行列とします。

CORRプロシジャは、影響を除去する変数に関連付けられている行に対してCholesky分解アルゴリズムを順番に適用することにより、で補正した後のの偏CSSCP行列であるを計算します。

変数に関連付けられている各行に対してCholesky分解アルゴリズムを適用した後、CORRプロシジャは、に関連付けられているすべての大きな番号の対角要素をチェックし、特異性が存在するかどうかを調べます。変数は、対応する対角要素のCholesky分解後の値が、その変数の元の修正済み平方和の倍よりも小さい値である場合は、特異と見なされます。特異性の基準を指定するには、SINGULAR=オプションを使用します。Pearson偏相関の場合、既に影響が除外された変数からこの変数を予測する際にがを超えるならば、コントロール変数は特異であると見なされます。これが発生する場合、CORRプロシジャはその変数を分析から除外します。同様に、コントロール変数から変数を予測する際にがを超えるならば、その変数は特異であると見なされます。これが発生する場合、それに関連付けられている対角要素、および対応する行または列内にあるすべての大きい番号の要素はゼロに設定されます。

に関連付けられているすべての行に対してCholesky分解アルゴリズムを適用すると、その結果として次の形式を持つ行列が生成されます。

ここで、は、、、である上三角行列です。

が正定値である場合、および偏CSSCP行列は、次の式から導かれる行列と同じになります。

偏分散/共分散行列は、分散算出用の分母を使用して計算されます(VARDEF=オプション)。CORRプロシジャは、偏分散/共分散行列に対して標準Pearson相関公式を適用することにより、Pearson偏相関行列を計算します。

相関行列が正定値である場合、単一変数zで補正後の変数xとy間の偏相関は、次に示す1次偏相関公式から導かれる相関と同じになります。

ここで、、、は適切な相関です。

より高次の偏相関の公式は、上記の1次偏相関公式を単純に拡張したものです。たとえば、相関行列が正定値である場合、z_1およびz_2で補正したxおよびy間の偏相関は、次に示す2次偏相関公式と同じになります。

ここで、、、は、指定の z_1における変数x、y、z_2間の1次偏相関です。

対応するSpearmanの偏順位相関およびKendallの偏tau-b相関を計算する場合、CORRプロシジャは、Spearmanの順位相関行列およびKendallのtau-b相関行列に対してCholesky分解アルゴリズムを適用し、対応する相関公式を使用します。すなわち、Spearmanの偏順位相関は、影響を除去した後の変数の順位にある、2変数の順位の線形回帰の残差間のPearson相関に等しくなります。このため、PARTIALステートメントでCORR=SPEARMANオプションを指定すると、2変数の順位の残差がプロットに表示されます。偏tau-b相関の範囲は–1～1です。ただし、この偏tau-b相関の標本分布は不明となるため、確率値は提供されません。

確率値

PearsonおよびSpearmanの偏相関の確率値は次の式により計算されます。

ここでは、自由度がのt分布に従います。は偏相関、は影響を除去する変数の数です。