概要:CORRプロシジャ

CORRプロシジャは、Pearsonの相関係数、3つのノンパラメトリックな相関統計量、Polyserialの相関係数、およびこれらの統計量に関連する確率を計算します。相関統計量には次のものがあります。

• Pearsonの積率相関

• Spearmanの順位相関

• KendallのTau-b相関係数

• Hoeffdingの従属統計量、

• Pearson、Spearman、およびKendallの偏相関係数

• Polyserialの相関係数

Pearsonの積率相関は、2つの変数間の線形関係についてのパラメトリックな統計量です。 Spearmanの順位相関は、データ値の順位に基づいて計算される連関性についてのノンパラメトリックな統計量です。Kendallのtau-bは、1対のオブザベーション内の一致と不一致の数に基づく、連関性についてのノンパラメトリックな統計量です。Hoeffdingの従属統計量は、より一般的な独立性からのずれを測る、連関性についてのノンパラメトリックな統計量です。偏相関は、他の変数による影響を補正した上で2つの変数間の相関を測定するものです。

Polyserialの相関は、1つの変数のみが直接測定される場合に、2変量正規分布を使用して2つの連続変数の相関を測定します。観測不能変数に関する情報は、観測不能変数の値を離散的な順序値の有限集合へと分類することにより導かれる1つの観測順序変数を通じて取得します。

関連するタイプの相関であるポリコリック相関(多分位相関)は、2変量正規分布を使用して、2つの観測不能変数間の相関を計算します。2つの観測不能変数に関する情報は、観測不能変数の値を離散的な順序値の有限集合へと分類することにより導かれる2つの対応する観測順序変数を通じて取得します。ポリコリック相関(多分位相関)は、CORRプロシジャでは使用できませんが、FREQプロシジャでは使用できます。

1セットの分析変数のみを指定した場合、デフォルトの相関分析では、分析変数ごとの記述統計量と、同変数のペアワイズ処理されたPearson相関統計量が計算されます。また、信頼性の指標であるCronbachのα係数も計算できます。

2セットの分析変数を指定した場合、デフォルトの相関分析では、分析変数ごとの記述統計量と、2セットの変数間のペアワイズ処理されたPearson相関統計量が計算されます。

Pearson相関やSpearman相関では、Fisherの変換を使用することにより、指定の帰無仮説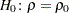の下でのその信頼限界と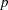値を導出できます。これらの統計量では、片側対立仮説または両側対立仮説を使用します。

2つの変数間の関係が非線形である場合、または外れ値が存在する場合、この相関係数は関係の強度を誤って推定することがあります。データをプロットすることにより、線形関係を検証し、潜在的な外れ値を特定できます。ODS Graphicsを有効にすると、アウトプットデリバリシステム(ODS)を通じて散布図と散布図行列を作成できます。また、散布図には、信頼楕円や予測楕円を追加できます。詳細は、信頼楕円と予測楕円のセクションを参照してください。

相関係数をSASデータセットに保存し、その他の統計およびレポート作成プロシジャで使用することができます。