CORRプロシジャ
例2.4 Fisherのz変換の応用
この例では、Fisherの 変換の応用を示します。詳細は、Fisherのz変換のセクションを参照してください。
変換の応用を示します。詳細は、Fisherのz変換のセクションを参照してください。
次のステートメントは、2変量正規分布から抽出した変数XとYの独立した標本をシミュレートします。150個のオブザベーションからなる最初のまとまりは、既知の相関0.3を使用して標本化されます。150個のオブザベーションからなる2番目のまとまりは既知の相関0.25を使用して標本化され、100のオブザベーションからなる3番目のまとまりは既知の相関0.3を使用して標本化されます。
data Sim (drop=i); do i=1 to 400; X = rannor(135791); Batch = 1 + (i>150) + (i>300); if Batch = 1 then Y = 0.3*X + 0.9*rannor(246791); if Batch = 2 then Y = 0.25*X + sqrt(.8375)*rannor(246791); if Batch = 3 then Y = 0.3*X + 0.9*rannor(246791); output; end; run;
このデータセットを使用して、Fisherの 変換の次のような応用を示します。
変換の次のような応用を示します。
母集団相関が指定の値に等しいかどうかテストする
2つの母集団相関が等しいかどうかテストする
異なる標本から計算した相関推定値を結合する
母集団相関が指定の値 に等しいかどうかのテスト
に等しいかどうかのテスト
次のステートメントを使用すると、両側対立仮説 に対する帰無仮説
に対する帰無仮説 の検定を実施できます。この検定は、オプションFISHER(RHO0=0.5)を使用して要求します。
の検定を実施できます。この検定は、オプションFISHER(RHO0=0.5)を使用して要求します。
title 'Analysis for Batch 1'; proc corr data=Sim (where=(Batch=1)) fisher(rho0=.5); var X Y; run;
出力2.4.1に、Fisherの変換に基づく結果を示します。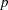 値が
値が 未満であるため、この帰無仮説は拒否されます。
未満であるため、この帰無仮説は拒否されます。
 である場合のFisherの検定
である場合のFisherの検定 | Analysis for Batch 1 |
| Pearson Correlation Statistics (Fisher's z Transformation) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| variable | With Variable | N | Sample Correlation | Fisher's z | Bias Adjustment | Correlation Estimate | H0:Rho=Rho0 | |||
| 95% Confidence Limits | Rho0 | p Value | ||||||||
| X | Y | 150 | 0.22081 | 0.22451 | 0.0007410 | 0.22011 | 0.062034 | 0.367409 | 0.50000 | <.0001 |
2つの母集団相関が等しいかどうかのテスト
次のステートメントを使用すると、2つの母集団相関 と
と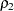 が等しいかどうかをテストできます。ここでは、帰無仮説
が等しいかどうかをテストできます。ここでは、帰無仮説 を、対立仮説
を、対立仮説 に対してテストします。
に対してテストします。
ods output FisherPearsonCorr=SimCorr; title 'Testing Equality of Population Correlations'; proc corr data=Sim (where=(Batch=1 or Batch=2)) fisher; var X Y; by Batch; run;
ODS OUTPUTステートメントは、表"FisherPearsonCorr"を、CORRプロシジャの出力データセット内に保存します。出力データセットSimCorrには、両方のまとまりに関するFisherの 統計量が含まれます。
統計量が含まれます。
次のステートメントは、図2.4.2のように、出力データセットSimCorrを表示します。
proc print data=SimCorr; run;
| Obs | Batch | Var | WithVar | NObs | Corr | ZVal | BiasAdj | CorrEst | Lcl | Ucl | pValue |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | X | Y | 150 | 0.22081 | 0.22451 | 0.0007410 | 0.22011 | 0.062034 | 0.367409 | 0.0065 |
| 2 | 2 | X | Y | 150 | 0.33694 | 0.35064 | 0.00113 | 0.33594 | 0.185676 | 0.470853 | <.0001 |
 をテストするための
をテストするための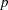 値は、差
値は、差 を平均がゼロで分散が
を平均がゼロで分散が の正規ランダム変数として扱うことにより導出されます。ここで、
の正規ランダム変数として扱うことにより導出されます。ここで、 と
と は、それぞれ標本相関
は、それぞれ標本相関 と
と に関するFisherの
に関するFisherの 変換です。また、
変換です。また、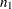 と
と は、対応する標本サイズです。
は、対応する標本サイズです。
次のステートメントは、出力2.4.3の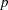 値を計算します。
値を計算します。
data SimTest (drop=Batch);
merge SimCorr (where=(Batch=1) keep=Nobs ZVal Batch
rename=(Nobs=n1 ZVal=z1))
SimCorr (where=(Batch=2) keep=Nobs ZVal Batch
rename=(Nobs=n2 ZVal=z2));
variance = 1/(n1-3) + 1/(n2-3);
z = (z1 - z2) / sqrt( variance );
pval = probnorm(z);
if (pval > 0.5) then pval = 1 - pval;
pval = 2*pval;
run;
proc print data=SimTest noobs;
run;
| n1 | z1 | n2 | z2 | variance | z | pval |
|---|---|---|---|---|---|---|
| 150 | 0.22451 | 150 | 0.35064 | 0.013605 | -1.08135 | 0.27954 |
出力2.4.3において、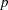 値0.2795は、帰無仮説
値0.2795は、帰無仮説 を拒否する根拠を提供しません。標本サイズ
を拒否する根拠を提供しません。標本サイズ および
および は、差
は、差 を有意水準
を有意水準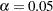 で検出するのに十分な大きさではありません。
で検出するのに十分な大きさではありません。
異なる標本から計算した相関推定値の結合
標本推定値 および
および は、それぞれ
は、それぞれ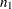 および
および というオブザベーションの2つの独立した標本から計算されます。結合された相関推定値は、
というオブザベーションの2つの独立した標本から計算されます。結合された相関推定値は、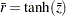 により与えられます。ここで、
により与えられます。ここで、  は、
は、 と
と の
の 変換の重み付きの平均です。
変換の重み付きの平均です。
 |
次のステートメントは、Batch1とBatch3を使用して、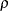 の推定値を計算します。
の推定値を計算します。
ods output FisherPearsonCorr=SimCorr2;
proc corr data=Sim (where=(Batch=1 or Batch=3)) fisher;
var X Y;
by Batch;
run;
data SimComb (drop=Batch);
merge SimCorr2 (where=(Batch=1) keep=Nobs ZVal Batch
rename=(Nobs=n1 ZVal=z1))
SimCorr2 (where=(Batch=3) keep=Nobs ZVal Batch
rename=(Nobs=n2 ZVal=z2));
z = ((n1-3)*z1 + (n2-3)*z2) / (n1+n2-6);
corr = tanh(z);
var = 1/(n1+n2-6);
zlcl = z - probit(0.975)*sqrt(var);
zucl = z + probit(0.975)*sqrt(var);
lcl= tanh(zlcl);
ucl= tanh(zucl);
pval= probnorm( z/sqrt(var));
if (pval > .5) then pval= 1 - pval;
pval= 2*pval;
run;
proc print data=SimComb noobs;
var n1 z1 n2 z2 corr lcl ucl pval;
run;
出力2.4.4に、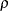 の結合された推定値を示します。この表は、結合された標本からの相関推定値が
の結合された推定値を示します。この表は、結合された標本からの相関推定値が であることを示しています。結合された推定値を使用する場合、
であることを示しています。結合された推定値を使用する場合、 の信頼区間は
の信頼区間は です。この信頼区間には、母集団相関
です。この信頼区間には、母集団相関 が含まれていることに注意してください。
が含まれていることに注意してください。
| n1 | z1 | n2 | z2 | corr | lcl | ucl | pval |
|---|---|---|---|---|---|---|---|
| 150 | 0.22451 | 100 | 0.23929 | 0.22640 | 0.10453 | 0.34156 | .000319748 |
