CORRプロシジャ
| KendallのTau-b相関係数 |
Kendallのtau-bは、1対のオブザベーション内の一致と不一致の数に基づく連関性についてのノンパラメトリックな統計量です。1対の変数の大小関係が同じである場合、一致が発生します。1対の変数の大小関係が逆転する場合、不一致が発生します。Kendallのtau-bは次の公式で表されます。
 |
ここで、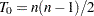 、
、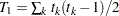 、
、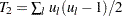 です。
です。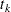 は結合された
は結合された 値の
値の 番目のグループ内にある結合された
番目のグループ内にある結合された の数、
の数、 は結合された
は結合された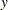 値の
値の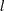 番目のグループ内にある結合された
番目のグループ内にある結合された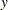 値の数、
値の数、 はオブザベーションの数です。
はオブザベーションの数です。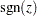 は次のように定義されます。
は次のように定義されます。
 |
CORRプロシジャは、データを順位付けし、Knight (1966)と同様の方法を使用することにより、Kendallのtau-bを計算します。最初の変数の値でオブザベーションを順位付けした後、2番目の変数の値でオブザベーションを順位付けすることにより、データが二重に並べ替えられます。CORRプロシジャは、最初の変数の並べ替え後の順位からKendallのtau-bを計算し、タイのペア(XまたはYの値が同じオブザベーションのペア)を修正します。


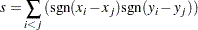
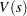 (
( の分散)は次の式で計算されます。
の分散)は次の式で計算されます。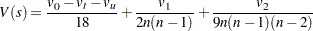
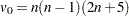


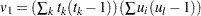
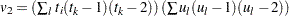
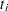 は結合された
は結合された は結合された
は結合された