CORRプロシジャ
| Fisherのz変換 |
標本相関 が相関
が相関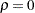 の2変量正規分布からの標本を使用する場合、次の統計量
の2変量正規分布からの標本を使用する場合、次の統計量
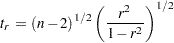 |
は、自由度が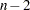 であるStudentの
であるStudentの 分布を持ちます。
分布を持ちます。
相関 の単調変換 (Fisher 1921)の場合、
の単調変換 (Fisher 1921)の場合、
 |
統計量 は、次の平均と分散を持つ近似正規分布を持ちます。
は、次の平均と分散を持つ近似正規分布を持ちます。
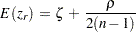 |
 |
ここで、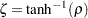 となります。
となります。
変換された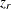 では、近似分散
では、近似分散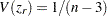 は相関
は相関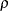 から独立になります。また、
から独立になります。また、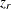 の分布が厳密な正規分布ではない場合であっても、
の分布が厳密な正規分布ではない場合であっても、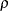 の任意の値の標本サイズが大きくなると、同分布は急速に正規性を持つようになります(Fisher 1970, pp. 200–201).
の任意の値の標本サイズが大きくなると、同分布は急速に正規性を持つようになります(Fisher 1970, pp. 200–201).
帰無仮説 で
で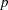 値を計算するには、次の式
値を計算するには、次の式
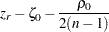 |
を平均がゼロで分散が の正規ランダム変数として取り扱います。ここで、
の正規ランダム変数として取り扱います。ここで、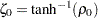 です(Fisher 1970, p. 207; Anderson 1984, p. 123) 。
です(Fisher 1970, p. 207; Anderson 1984, p. 123) 。
CORRプロシジャでは、帰無仮説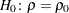 に基づいて
に基づいて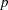 値を計算する場合、バイアス調整
値を計算する場合、バイアス調整 が必ず使用されます。
が必ず使用されます。
FISHERオプション内のALPHA=オプションは、信頼水準 の値
の値 を指定します。RHO0=オプションは、帰無仮説
を指定します。RHO0=オプションは、帰無仮説 での値
での値 を指定します。BIASADJ=オプションは、信頼水準でバイアス調整を使用するかどうかを指定します。
を指定します。BIASADJ=オプションは、信頼水準でバイアス調整を使用するかどうかを指定します。
TYPE=オプションは、信頼限界のタイプを指定します。TYPE=TWOSIDEDオプションは、帰無仮説 の下での両側信頼限界と
の下での両側信頼限界と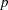 値を要求します。片側信頼限界の場合、TYPE=LOWERオプションは、帰無仮説
値を要求します。片側信頼限界の場合、TYPE=LOWERオプションは、帰無仮説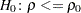 の下での下側信頼限界と
の下での下側信頼限界と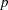 値を要求します。TYPE=UPPERオプションは、帰無仮説
値を要求します。TYPE=UPPERオプションは、帰無仮説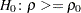 の下での上側信頼限界と
の下での上側信頼限界と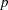 値を要求します。
値を要求します。
相関に対する信頼区間
相関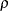 の信頼限界は、バイアス調整の有無にかかわらず、パラメータ
の信頼限界は、バイアス調整の有無にかかわらず、パラメータ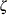 の信頼限界を通じて導かれます。
の信頼限界を通じて導かれます。
バイアス調整を行わない場合、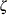 の信頼限界を計算するには、次の式
の信頼限界を計算するには、次の式
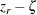 |
が平均ゼロで分散 の正規分布を持つものとして扱います。
の正規分布を持つものとして扱います。
すなわち、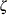 の両側の信頼限界は次のように計算されます。
の両側の信頼限界は次のように計算されます。
 |
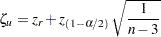 |
ここで、 は標準正規分布の
は標準正規分布の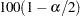 番目のパーセント点です。
番目のパーセント点です。
バイアス調整を行う場合、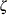 の信頼限界を計算するには、次の式
の信頼限界を計算するには、次の式
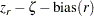 |
が平均ゼロで分散 の正規分布を持つものとして扱います。ここで、バイアス調整関数(Keeping 1962, p. 308)は次のようになります。
の正規分布を持つものとして扱います。ここで、バイアス調整関数(Keeping 1962, p. 308)は次のようになります。
 |
すなわち、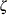 の両側の信頼限界は次のように計算されます。
の両側の信頼限界は次のように計算されます。
 |
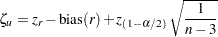 |
続いて、上記の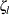 および
および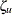 に関して計算された信頼限界の変換を元に戻すことにより、相関
に関して計算された信頼限界の変換を元に戻すことにより、相関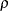 の信頼限界が導かれます。
の信頼限界が導かれます。
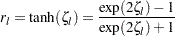 |
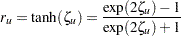 |
バイアス調整を行う場合、CORRプロシジャは次のような相関推定値も表示します。
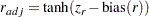 |
Fisherのz変換の応用
Fisher (1970, p. 199)は、次に示すような 変換の具体的な応用を紹介しています。
変換の具体的な応用を紹介しています。
母集団相関が指定の値に等しいかどうかのテスト
2つの母集団相関が等しいかどうかのテスト
異なる標本から計算した相関推定値の結合
オブザベーション数が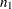 で標本相関が
で標本相関が である標本からの母集団相関
である標本からの母集団相関 が、与えられた
が、与えられた に等しい場合、まず
に等しい場合、まず および
および :
: 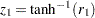 および
および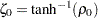 に対して
に対して 変換を適用します。
変換を適用します。
続いて、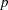 値を計算するには、次の式
値を計算するには、次の式
 |
を平均ゼロで分散 の正規ランダム変数として扱います。
の正規ランダム変数として扱います。
標本推定値 および
および は、それぞれ
は、それぞれ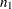 および
および というオブザベーションの2つの独立した標本から計算されます。2つの対応する母集団相関
というオブザベーションの2つの独立した標本から計算されます。2つの対応する母集団相関 および
および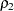 が等しいかどうかをテストするには、まず
が等しいかどうかをテストするには、まず 変換を2つの標本相関である
変換を2つの標本相関である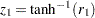 および
および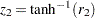 に対して適用します。
に対して適用します。
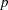 値は、等しい相関の帰無仮説の下で導かれます。すなわち、差
値は、等しい相関の帰無仮説の下で導かれます。すなわち、差 は、平均がゼロで分散が
は、平均がゼロで分散が である正規ランダム変数として分布されます。
である正規ランダム変数として分布されます。
さらに、2つの標本が同じ相関をもつ母集団から抽出されたと仮定すると、結合された相関推定値を計算できます。対応する 値の重み付き平均は次の式で表されます。
値の重み付き平均は次の式で表されます。
 |
ここで、重みは、それらの分散に対して反比例します。
このため、結合された相関推定値は、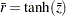 および
および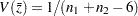 となります。これらの応用に関する詳細は、例2.4を参照してください。
となります。これらの応用に関する詳細は、例2.4を参照してください。
なお、このアプローチは、複数の標本を含めるように拡張できます。
