随想「マーケティングとデータ解析」
第4回 主成分への回帰の不思議
朝野熙彦
中央大学客員教授
マーケティングの現場でデータ解析をしていると、統計学の素晴らしさに感動する時もたまにありますが、疑問を感じることもしばしばです。今回は疑問を感じる話として主成分への回帰について想い出話をしましょう。
INDEX
1.要因のウェイトを知りたい
随想の第1回で、何の因果か私がマーケティングの世界で働くことになった話をしました。今回はその続きです。
【ウェイトを知りたいという欲求】
企業を回って御用聞きをしていた頃のことです。複数の要因があって、それぞれの重みを知りたいのだがどうしたらよいのか?というご質問をよく受けました。ウェイトとか重要度とか呼び方は様々ですが、その解釈は一緒です。企業の方は自社品が売れればそれでいいと言います。誠にその通りですが、現実には企業が満足するほど売れることなどめったにありません。むしろ期待を裏切ってしまうことが多いものです。すると企業としては、その理由を知りたくなります。つまり販売実績を知っただけでは何の情報価値もないわけで、不振の原因が何かが分からなければ打つべき対策が見えてきません。
質問をする側もデータ解析の素人ですが、答える私も素人です。どうしたらいいのだろう?重回帰分析で答えが出せるのだろうか?と悩んだものです。
当時この議論のベンチマークとして良くとりあげられたのがCS(customer satisfaction, 顧客満足)の調査・コンサルティングで有名な米国の J.D. パワー社でした。
同社では自動車のモデル別、メーカー別のCSI(顧客満足度指標)を1980年から公表していました。自動車の再購入意図とCSの関係が大きいことを論拠にCSこそがビジネスの原点であると言われたものです。同社の CSIの作り方は顧客満足の総合評価を基準変数にして、その原因系として技術と人的サービスの2つの説明変数を設定したもので、『CSI=技術+人的サービス』というのが基本的なモデルでした。その概要は1990年4月26日の日経産業新聞に紹介されています。
具体的にどのようにインデックスを作成したのかというと、たとえば1986年の調査では145の自動車のモデルを23個の変数で評価させて、その平均値を求めます。次に145行23列の平均値データ行列を因子分析して2因子を抽出して因子得点のベクトルf1,f2を推定します。最後に図1のように顧客満足度のベクトルyを2因子によって張られる因子空間S(F)に射影するという仕組みでした。ベクトル が顧客満足度のモデル値になります。図1のeは残差ベクトルです。
が顧客満足度のモデル値になります。図1のeは残差ベクトルです。
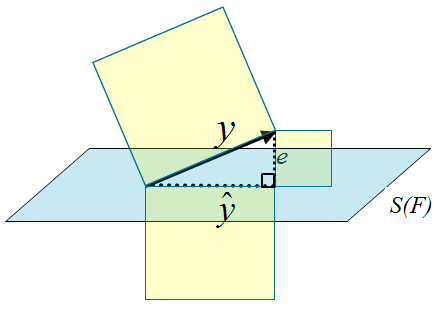
図1 因子空間への回帰の図
J.D. パワー社の社長J.D.Power3世自身が1990年に来日してCSIのセミナーを開きました。セミナーのTechnical description of the indexの資料には、cを定数にして次のような趣旨の予測式が書かれています。

彼らが行った因子分析は直交解でしたので、直交空間への回帰によって2つの要因の重みを求めたことになります。このように全体的な結果に及ぼす個別要因の重みを知りたいという欲求は、サービス分野だけでなく製品開発の分野でも出てきます。たとえば製品の総合評価を決めるのはデザインなのか性能なのかという議論は、様々な製造業で交わされる議論でしょう。
【重みを知るという意味】
要因が2因子だけという事態はごくまれで、現実には多数の要因が考えられます。それらを説明変数 と書きましょう。かりに重回帰分析をしたとして、p個の変数に対応した偏回帰係数を
と書きましょう。かりに重回帰分析をしたとして、p個の変数に対応した偏回帰係数を 、標準偏回帰係数を
、標準偏回帰係数を と書きましょう。さて重みを知りたいというマーケターの欲求を整理しますと表1のようになります。
と書きましょう。さて重みを知りたいというマーケターの欲求を整理しますと表1のようになります。
| 疑 問 | 具体的にいうと | 情報の水準 |
| 1)重要な要因なのかどうか | 説明変数を重要グループと非重要グループの2群に分ける | 名義尺度 |
| 2)重要な順序を知る | 説明変数を重要度でランキングする | 順序尺度 |
| 3)重要度に差があるのか | 変数のペアについて重要度に差があるか否か | 同順位を認める順序尺度 |
| 4)重要度の構成比を知りたい | 説明変数の全体を100%としたときに各説明変数の重要度が何%ずつになるか | 比率尺度 |
表1 重みを知る
問題があるなら正解があるはずだ、と信じるのは日本の初等教育の弊害です。問題はあっても正解がないことなどは科学でも社会でもいくらでもあります。また表1の整理は人間の知識に対する向上心も教えてくれます。たいていの方は1)の名義尺度の水準から次第に4)の比率尺度の水準へと知識欲求を高めていくものです。
2.一筋縄ではいかない
【実務の現場で湧きあがる疑問】
疑問1)に対する具体策としては、帰無仮説を偏回帰係数=0とおいて、統計的に有意なら無駄な説明変数とはいえないだろう、という解釈があります。積極的に重要であるとも言えないわけですが、こんな消去法の判断でもよいのかもしれません。
しかし疑問2)から先は話がずっと難しくなります。仮に だとしますと、パラメータが大きい順に
だとしますと、パラメータが大きい順に の方が
の方が より重要だと理解してよいのでしょうか?
より重要だと理解してよいのでしょうか? はyを高め、
はyを高め、 はyを下げるとしても、その効き目は違います。とくにマーケティングの場合は、消費者の意識を扱うだけに、しばしば符号に不定性があります。たとえばデザインのイメージ尺度の例をあげますと、
はyを下げるとしても、その効き目は違います。とくにマーケティングの場合は、消費者の意識を扱うだけに、しばしば符号に不定性があります。たとえばデザインのイメージ尺度の例をあげますと、
| スコア(1) | スコア(2) | |
|---|---|---|
| 非常に革新的 | -2 | 2 |
| やや革新的 | -1 | 1 |
| どちらともいえない | 0 | 0 |
| やや伝統的 | 1 | -1 |
| 非常に伝統的 | 2 | -2 |
「革新-伝統」のイメージ尺度に対して、昇順のスコア(1)を当てようが降順のスコア(2)を当てようが任意のはずです。しかし符号を反転すれば だった推定値は
だった推定値は に変わります。したがってスコアリング次第で重要度のランキングも変わってしまうのです。
に変わります。したがってスコアリング次第で重要度のランキングも変わってしまうのです。
それなら と絶対値をとって、
と絶対値をとって、 よりも
よりも の方が重要だと解釈すればいいのでしょうか。しかし2つの変数に因果関係があった場合はそう単純には言い切れないかもしれません。
の方が重要だと解釈すればいいのでしょうか。しかし2つの変数に因果関係があった場合はそう単純には言い切れないかもしれません。
表1の疑問4)も悩ましい問題です。単純に標準偏回帰係数の比をとれば済むというなら変数1の重要度は、直上の数値例の場合、
 ですし、同様の計算で変数2の重要度は200になります。これは重要度の構成比として全く意味が通じない指標です。絶対値の比をとる計算も機械的な計算としてなら出来ますが、それが重要度の構成比を意味するという統計的な裏付けはありません。
ですし、同様の計算で変数2の重要度は200になります。これは重要度の構成比として全く意味が通じない指標です。絶対値の比をとる計算も機械的な計算としてなら出来ますが、それが重要度の構成比を意味するという統計的な裏付けはありません。
実務の現場ではこのように素朴な疑問から議論が湧きあがるものです。データ解析の実務で大切なことは、回帰分析の計算手順を覚えることでもなければ、パソコンの操作を覚えることでもありません。アウトプットが何を意味するかについてユーザーが理解することこそが肝心なのです。広告部門と販促部門は予算配分で対立することがあります。ですから複数の要因のどちらが重要かという議論は、純学術的な問題を越えて、セクション間の利害対立にまで発展するのです。
1960年代、70年代に出版されたリサーチの手引書には、こうしたユーザーの悩みを置き去りにして計算手順の記述だけに終始した無意味なマニュアル本が多かったように思います。
【何がネックになっているのか】
説明変数の重みが線形のモデルに従ってすっきり分解できない理由は、説明変数に相関があるからです。そのため相乗効果や相殺効果が発生して、何がなにやら判断できなくなるのです。
図1では基準変数のyが と分解されて、それに応じてyの分散が
と分解されて、それに応じてyの分散が の分散とeの分散の和に分解できます。そのわけは、図1の三角形の
の分散とeの分散の和に分解できます。そのわけは、図1の三角形の とeが直交しているからなのです。三平方の定理が分散の分解の根拠になります。J.D. パワーの①式ではベクトルf1,f2が直交しますから、2つの因子の重みは2つのβの値の2乗の構成比によって評価できます。それが各説明変数の受け持つ分散比を意味するからです。
とeが直交しているからなのです。三平方の定理が分散の分解の根拠になります。J.D. パワーの①式ではベクトルf1,f2が直交しますから、2つの因子の重みは2つのβの値の2乗の構成比によって評価できます。それが各説明変数の受け持つ分散比を意味するからです。
けれども、通常マーケティングに出てくる説明変数は互い相関があって当たり前です。極端に相関係数が高いと偏回帰係数の標準誤差が極めて大きくなってパラメータの精度が悪化します。このような病的な状態を俗語でマルチコと呼んでいます。きちんといえば多重共線性(multicollinearity)です。
つまり要因の重みを知るという問題は、どのように原データを無相関、あるいは無相関に近いデータに変換して回帰分析するのか?という問題に帰着するのです。統計学の本には古来、多くの工夫が提案されてきたことが書かれています。リッジ回帰やスペクトル分解などいろいろありますが、いずれも厳密な論拠に欠けるように感じられました(注1)。中でも私がトリッキーな方法だと思ったのが主成分への回帰でした。
3.偶然にかける一縷の望み
【主成分への回帰とは】
RPC(Regression on Principal Component,主成分への回帰)の説明をしましょう。あくまでも本稿はエッセーなので、煩わしければ数式部分は読み飛ばしてくださって結構です。
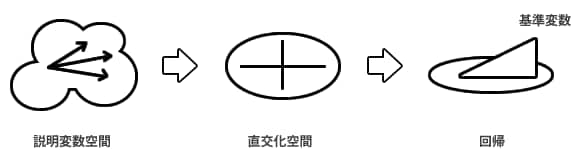
図2 主成分への回帰の図
n行p列の平均偏差データ行列をXとして主成分スコア行列がF=XWで与えられたとします。行列は大文字ゴシックの斜体で書きましょう。主成分は分散共分散行列 の固有値が大きい順にr個までで打ち切るとします。順にr個の固有ベクトルを並べたp行r列の行列がWです。Fによって基準変数yを予測する偏回帰係数をhとすれば、yの予測値は次式のように表現できます。なおベクトルは小文字のゴシックの斜体で区別します。
の固有値が大きい順にr個までで打ち切るとします。順にr個の固有ベクトルを並べたp行r列の行列がWです。Fによって基準変数yを予測する偏回帰係数をhとすれば、yの予測値は次式のように表現できます。なおベクトルは小文字のゴシックの斜体で区別します。

ここで②の右辺のXから先の部分をg = W(F' F )-1 F'yとまとめて書きましょう。本稿ではこれをRPCウェイトと呼びましょう。gは行列Wとベクトルhの掛け算で求められますので、電卓やEXCELで簡単に計算できます。②をgを使って表しますと、

回帰分析で偏回帰係数を推定する②式の段階では、元々のp個よりも少ないr個の説明変数を使いますし、しかも説明変数である主成分は直交しています。ですから原データのXを使った回帰分析よりも望ましい状況で回帰分析をしていることになります。にもかかわらず、③においてXに掛けられる係数ベクトルgが導けます。抽象的な主成分ではなく、元々の説明変数に対応した係数が分かるので、具体的にウェイトが理解できます。なお③の予測式の決定係数は②の回帰分析と同じです。
【直観に訴える望ましさ】
問題は、通常の重回帰分析(OLSと呼びましょう)から得られるbと主成分への回帰から得られるgのどちらが良いのか?ということです。
全く経験的な話で恐縮ですが、gの方が納得のいく結果が得られやすいという印象をもちました。好きなテレビタレントのイメージを分析すると、OLSよりもRPCの方が「セクシーな」の順位が上がりました。「センスがいい」と「現代的な」はマイナスからプラスに変わりました。
またスキー板の購入意向の分析ではOLSでは「ダサい」の回帰係数が高かったのに対して、RPCでは「プロっぽい」や「カッコいい」の係数が高くなりました。
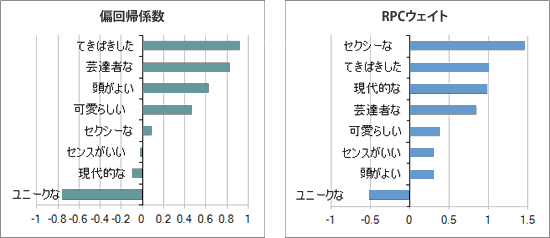
図3 テレビタレントの好感度
理由はともかく納得がいく結果が出ることは実務では歓迎されるものです。
もちろんRPCにも欠陥があって、②の回帰においては原データXの情報のすべてを使っていないことがあげられます。主成分でいえば固有値が小さい に対応した情報はゴミ扱いして捨てています。r番目までの主成分の累積寄与率を
に対応した情報はゴミ扱いして捨てています。r番目までの主成分の累積寄与率を として、この率が80%を上回ったら打ち切る、という基準を用いることもあります。問題は「どこでカットすべきか」という根拠があいまいなことにあります。この問題はRPCに限らず、通常の主成分分析や因子分析でも固有値の小さい次元をカットするので同じことです。多変量解析は次元の圧縮をしているのだから、主要でない次元を捨てることは正当化できるという説もあります。
として、この率が80%を上回ったら打ち切る、という基準を用いることもあります。問題は「どこでカットすべきか」という根拠があいまいなことにあります。この問題はRPCに限らず、通常の主成分分析や因子分析でも固有値の小さい次元をカットするので同じことです。多変量解析は次元の圧縮をしているのだから、主要でない次元を捨てることは正当化できるという説もあります。
マーケティングの実務では説明のしやすさとかグラフ表現のしやすさを優先して2次元までで打ち切ることが少なくありません。実務では次元圧縮による損失の見積もりをあまり気にかけないように感じました。
4.綱渡りのようなトリック
【厳密さの追求】
厳密さを追求するとどうなるのでしょうか。当時、あるマーケターから主成分を全根出してRPCウェイトを正確に計算してください、と注文されたことがあります。
実際に計算してみれば分かることですが、どうなるかを説明しましょう。ここではp個の主成分得点を並べた行列をF、対応する主成分係数の行列をWとします。

④がRPCウェイト、⑤は分散共分散行列のスペクトル分解で、Λは固有値を主対角要素とするp次の対角行列、⑥はその逆行列を示します。⑦で固有値とは主成分スコアの分散に他ならないことを示していますが、そこではW'W=Iという性質を使っています。⑧でその逆行列を用意しておきます。⑤から⑧まではすべて主成分分析について既知の性質です。
以上の準備のもとに④の右辺に⑧と⑥を代入して展開すると、gがOLSの偏回帰係数bに一致することが証明できます。

厳密さを追求するとOLSの解に帰着するので、主成分に回帰する意味がなくなる、というのがこと真相です。あえて全根を出さないという「綱渡りのようなサジ加減」にRPCの醍醐味があります。
【主成分の選択】
なお各主成分の重要度は固有値で評価されると言いながらも、基準変数yを予測することが最終目的ですから、固有値は説明変数としての重要性を意味しません。第1主成分を飛ばして、その先の主成分に予測の上で重要な主成分があってもおかしくないのです。これもRPCと主成分の打ち切り基準の間に整合性がなくて悩ましい問題です。全根の主成分スコアFを出しておいて、変数選択の回帰分析を行えば、主成分のあいまいな打ち切り基準を避けることができるかもしれません。いずれにしても試行錯誤をして納得しやすいgを探すことになります。
【まとめ】
J.D.パワーも、③と似たような計算を因子分析にあてはめて個々の説明変数のウェイトを導きました。ですから「因子分析への回帰」もRPCと同様にできるのです。ただし、因子分析には共通性の推定と回転法にそれぞれバリエーションがたくさんあるために、データ解析の全プロセスを正確に開示しない限り、他者が分析結果を再現できません。
因子分析があいまいだとか主成分分析より劣っている、という意味ではありません。ただ因子分析の方が主成分分析より複雑だ、というだけのことです。
さて、私はマーケティングの現場の方々との議論を通じて要因のウェイトを評価することの難しさを実感しました。そのために無相関のデータを計画的に生成することに関心を持つようになりました。その関心の延長上にコンジョイント分析があったのです。コンジョイント分析についてはいずれ稿をあらためて随想したいと思います。
(注1)次の本でマルチコの発見法を3通り、マルチコの対策を8通り紹介しています。
朝野熙彦『入門多変量解析の実際 第2版』講談社 2000年10月20日
参考書籍
『入門多変量解析の実際 第2版』
【著者】朝野熙彦 【出版社】講談社 【サイズ】A5判 【ページ数】206ページ
【価格】2,940円 【発売日】2000年10月20日 【ISBN】978-4-06-153963-1
【目次】
1 ウォーミングアップ ~下準備と本書のパノラマ~
2 コレスポンデンス分析と数量化理論 III 類 ~製品やブランドをポジショニングする~
3 主成分分析 ~情報を集約する~
4 因子分析 ~隠された構造を可視化する~
5 クラスター分析 ~新しいセグメントを発見する~
6 重回帰分析と数量化理論 I 類 ~市場性を予測する~
7 正準相関分析と判別分析 ~多変量解析の総本山に迫る~
8 コンジョイント分析 ~新製品のコンセプトを開発する~
9 トラブル・シューティング
10 ユーザーのための多変量解析