Expertentipp:
Wussten Sie schon, wie Sie mit SAS getrimmte und winsorisierte Mittelwerte berechnen können?
Und so geht’s:
Das getrimmte und das winsorisierte Mittel sind sogenannte robuste Lagemaße. Beide Statistiken tragen der Situation Rechnung, dass im Rahmen einer Stichprobenziehung erfasste Werte durch Ausreißer an den Rändern der empirischen Verteilung „verunreinigt“ sein können.
Für das getrimmte bzw. gestutzte Mittel werden die k kleinsten und die k größten Werte entfernt. D. h. in einer Stichprobe vom Umfang n ergibt sich das getrimmte Mittel einer metrischen Variablen x als arithmetischer Mittelwert aus den n - 2k „mittleren“ Werten in der geordneten Urliste von x.
Im Unterschied dazu werden beim Winsorisieren die k kleinsten Werte von x durch den (k+1)-sten und die k größten Werte von x durch den (n-k)-ten Wert in der geordneten Urliste von x ersetzt. Die Berechnung des winsorisierten Mittels erfolgt dann in Form des arithmetischen Mittelwertes auf diesen modifizierten n Beobachtungen.
SAS bietet mit den Optionen TRIMMED= und WINSORIZED= in der Prozedur UNIVARIATE eine einfache Möglichkeit, das getrimmte und das winsorisierte Mittel einer metrischen Variablen zu berechnen. Der folgende Aufruf der Prozedur UNIVARIATE verdeutlicht die Verwendung dieser beiden Optionen:
ods select TrimmedMeans WinsorizedMeans;
proc univariate data=sashelp.heart trimmed=1 0.1 winsorized=0.1;
var systolic;
run;
Mit der TRIMMED=-Option werden zwei getrimmte Mittelwerte berechnet; der erste unter Entfernung der kleinsten und der größten Beobachtung der Variablen SYSTOLIC (systolischer Blutdruck), der zweite unter Entfernung der 10% kleinsten und 10% größten Werte von SYSTOLIC. Nachstehend wird der ent¬sprechende durch die Prozedur UNIVARIATE erzeugte Output dargestellt:
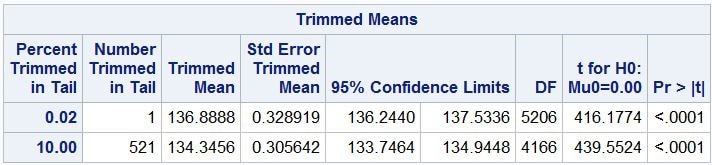
Über die WINSORIZED=-Option wird das winsorisierte Mittel der Werte von SYSTOLIC berechnet, wobei jeweils 10% der Beobachtungen in den Rändern der empirischen Verteilung durch den nächstgrößeren bzw. -kleineren Wert aus den restlichen Daten ersetzt werden. Die nachstehende Tabelle zeigt den zugehörigen durch die Prozedur UNIVARIATE erzeugten Output:
Weitere Tipps zum Thema erhalten Sie im Kurs Statistik 1: Varianzanalyse, Regression und logistische Regression.
