随想「マーケティングとデータ解析」
第10回 コレスポンデンス分析
朝野熙彦
中央大学客員教授
SAS Technical News Summer 2012号からスタートした本連載も今回をもって最終回にしたいと思います。2年半にわたり私の拙い文章を掲載してくださったSAS社の度量の大きさに敬服いたします。さて、これまでは主にマーケティングの現場での苦労話を紹介してきましたので、今回はあるデータ解析にまつわる想い出話をしようと思います。
1.コレスポンデンス分析
今回の話題はポジショニング分析でよく使われているコレスポンデンス分析です。実務の世界では、しばしば「コレポン」と略称されていますが、それはフォーカス・グループ・インタビューをグルインと呼ぶのと同様の業界俗称です。私はきちんとコレスポンデンス分析という方が好きです。
さてコレスポンデンス分析では表1のようなクロス表とか２元表（2-way contingency table）と呼ばれるデータを分析します。表１は４つのブランドがそれぞれ３つのイメージ変数に該当すると回答した人数だと思ってください。
| 列 | ||||
| イメージ１ | イメージ２ | イメージ３ | ||
| 行 | ブランドA | 1 | 1 | 2 |
| ブランドB | 0 | 3 | 1 | |
| ブランドC | 2 | 2 | 4 | |
| ブランドD | 1 | 0 | 3 | |
表1 原データ行列Z
コレスポンデンス分析をすると、行列の各行と各列にスコアが与えられます。その与え方が行数をp、列数をqとすれば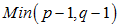
だけあるので、表1の場合は２次元の解が求められます。そこで第1次元のスコアを横座標、第２次元のスコアを縦座標にとってプロットすると図1、図2のようになります。ふつう前者をブランド空間、後者をイメージ空間と呼んでいます。図1のⅠ次元とⅡ次元、図2のⅠ’次元とⅡ’次元はそれぞれ直交しています。ですから座標軸が直角に交わるように図を描いたのは、ただの便宜上の話ではなく数学的な根拠があるのです。
またⅠとⅠ’というように一方にプライムをつけて次元を区別した理由は、それらが同一の座標軸ではないからです。
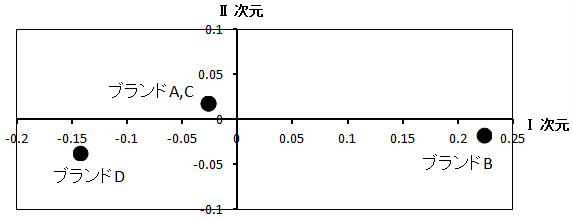
図1 ブランド空間
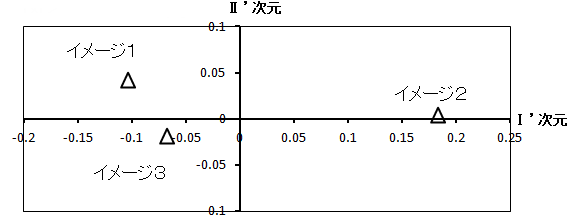
図２ イメージ空間
コレスポンデンス分析のプログラムを付録に示しました。最低限のデータ解析はこれで終わりなので分析作業そのものは簡単です。
次節以降でコレスポンデンス分析をめぐる様々な疑問と、そうした疑問を通じてデータ解析への関心が強くなったという自分の想い出についてお話ししたいと思います。
2. 素朴な疑問が芽生える
■ルーツはどこにあるのか
ベンゼクリ（1973）のコレスポンデンス分析を知って私がまず疑問に思ったのは、この分析は日本で有名な林（1952）の数量化理論Ⅲ類と同じではないか？というものでした。
私が仕事を始めた1970年代は統計数理研究所の林知己夫先生が提唱された数量化理論が日本のマーケティング界でもてはやされていた時代です。数量化理論の総称のもとに多くのモデルが開発されましたが、その一つがⅢ類でした。
Ⅲ類は複数のカテゴリーへの反応パターンを意味する矩形行列が与えられた時に、行と列に最適なスコアを与えようとするものです。Ⅲ類では行列の要素をYesなら１、Noなら0のダミー変数で記述するのですが、表１のZであっても1-0は扱えますから、それは両者の本質的な相違ではありません。
さて、私は多変量解析を知らなかったものですから、文献をいくつか当たってみたところ、類似した分析モデルがいくつも存在することを知りました。
その頃、Guttman(1941)、Mosteller(1949)、林（1952）、芝 (1965､a,b）の合計5種類のモデルを比較したメモ書きがあります（朝野、1974）。どの方法も固有値問題に帰着するので、モデル間で固有値と固有ベクトルが互いにどう関連付けられるかを整理したものです。
後になって当時の文献サーベイが全く不十分だったことを思い知らされました。たとえば西里 (2007,pp64-65.)によれば、２元表の行と列を数量化しようという研究は20世紀初頭から各国の研究者によって始まり、スケーログラム法、交互平均法、最適尺度法、双対尺度法など名称の異なる52種類もの分析法として繰り返し発見されてきたそうです。応用場面が違う、目的関数が異なる、データの制約条件と規準化の仕方が異なるなどの相違がありますから、それらの分析が完全に同一だと西里先生が言っているわけではありません。数学的な本質が同等だと言っているのです。
分析法を誰が最初に言い出そうがそんなことはどうでもいいじゃないか、というのがビジネスの世界での常識でした。ですから、コレスポンデンス分析のルーツ探しなどは変人がすることだと私は奇異に見られていたようです。
私自身としては、様々な多変量解析が固有値問題に帰着すること、そして表1の行列なら２次形式の最大化問題になるという、これまた専門家なら誰でも知っていた当然の事実を、そうだその通りだと初心者らしく納得していた時期でした。
ところでどういうわけで類似した分析法がたくさん生まれてしまったのかという疑問への私なりの結論ですが、それは応用目的に応じて発展するというデータ解析ならではの性格にあると思います。生物の先生、考古学の先生と行動科学の先生が同じ学会で研究を発表しあうという場面はほとんどありません。ですからほぼ同じ分析法が各学問分野で独立に開発されてしまったのでしょう。もう一つは２元表は日ごろなじみの深いデータだという理由にあります。そのため２元表を最適スコアリングするという研究テーマは、多くの研究者にとって魅力的だったのでしょう。
■行スコアの空間と列スコアの空間の関係
図1の第Ⅰ次元と図２のⅠ’次元そして、図1の第Ⅱ次元と図２のⅡ’次元は同じ次元か、という疑問です。これについては竹内・柳井（1983,p.163）と柳井（1994）が示しているように、２つの空間には図３のような乖離（discrepancy）があることが知られています。
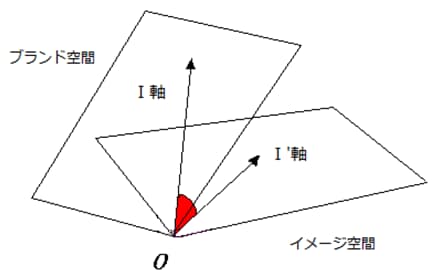
図３ 正準相関分析の幾何学的表現
２組の空間でそれぞれベクトルを自由に動かして両者の角度θが最も小さくなった時のベクトルをⅠ軸、Ⅰ’軸にするという幾何学的なイメージです。２つの軸の角度θが最小ということは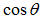
が最大ということであり、
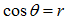ですから、２つの部分空間の正準相関係数を最大化することと等しい、という理屈です。しかもその正準相関係数は特異値に他ならないことが分かっています（Gifi 1990,ｐ.273）
ついでながら第２次元の軸がどのように定まるのかを図示したのが図４です。表1のデータの場合、正準相関係数は図3で0.538、図4で0.104になります。角度に直せばそれぞれ57.5度、84度です。正準相関係数が小さくなるほど、ブランド空間とイメージ空間が乖離していくわけです。
表4に4次元空間における座標軸間の相関係数を整理しました。
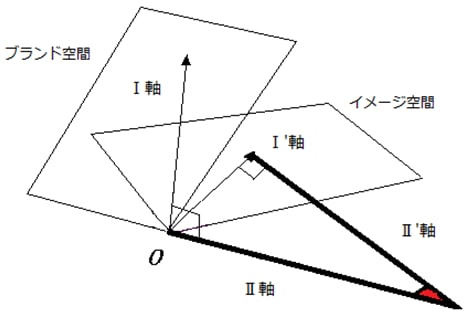
図４ ２次元目の幾何学的表現
| Ⅰ | Ⅱ | Ⅰ’ | Ⅱ’ | |
| Ⅰ | 1 | 0 | 0.538 | 0 |
| Ⅱ | 0 | 1 | 0 | 0.104 |
| Ⅰ’ | 0.538 | 0 | 1 | 0 |
| Ⅱ’ | 0 | 0.104 | 0 | 1 |
表２ 4つの座標軸の正準相関係数
特異値が１でない限り行スコアと列スコアは同一のユークリッド空間に属さないことを西里（2014,p.98）が指摘しています。この問題で利用者の誤解を招いてきたのが、多次元の解をスコア行列A,Bで表したときに、一方のスコアから他方のスコアが計算できることでした。①,②では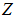
の行和からなる対角行列を
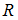、列和からなる対角行列を
、 
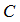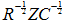の特異値からなる対角行列を
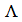で表しています。
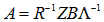………………………………………①
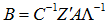………………………………………②
①②は変換公式（transition formula）あるいはフランス学派ではsubstitution formulaと呼ばれています。
では線形変換されたベクトルであれば変換元のベクトルと同一空間に属するといえるのか、といえばそれは正しくありません。
分かりやすい例をあげてみましょう。重回帰分析のモデルは図5のように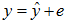
と表せます。ここで
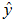は基準変数ベクトル
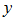を説明変数の空間
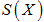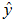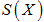に射影したベクトルです。当然ながらは空間に属します。しかし基準変数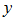は一般に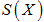に属しません。 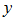は空間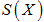を張らない、という言い方もできます。
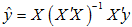………………………………………③
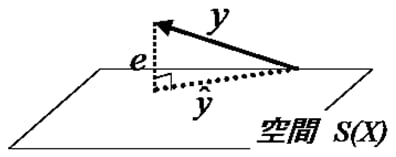
図5 重回帰分析の図解
なおスコア行列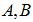 
だけの情報では原データ 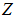が再生できないことを④の再生公式(reproduction formula)が示しています。このことは図1,2の情報だけでは表1が復元できないという、グラフィック表現の限界を意味しているのです。
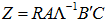………………………………………④
■ブランドとイメージ変数間の距離
図１におけるブランド間の平方距離は、Zにある種の調整をしたプロフィール間で測った平方距離と厳密に一致することが知られています。ここでいう平方距離とはユークリッド距離の平方のことで、２点を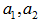
とすれば
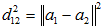………………………………………⑤
で求められる量です。
図２のイメージ変数間の距離も、図１とは異なる調整をしたプロフィール間の距離と一致します（Gifi、1990)。付録のプログラムの後半ではプロフィールの作成と距離計算を行っています。
以上の根拠にもとづいて各プロット間の距離が原データの何の情報を表しているかが合理的に説明できます。実はコレスポンデンス分析をしなくても、電卓やEXCELを使うだけで同じ相内の点間距離が原データからダイレクトに手計算できるのです（朝野、2010）。
問題はブランドとイメージを組み合わせた２相点間距離です。私が２相点間距離の測定に関心を持ったのが1990年代でした。
そもそも別な空間に属する2点間の距離をどう定義したらよいのでしょう。たとえばブランドのプロットをイメージ空間に射影する非対称スケールや、論争を巻き起こしたCarrollら（1986）のCGSスケールなどが提案されましたが理論面や実用面で欠点があって普及しませんでした。擬似コンティンジェンシー表を規準化したうえで特異値分解する方法も可能で、CGSスケールよりも性質の優れた距離を導くことができます（朝野、2008）。
近年になって解の次元が増えてしまうものの、厳密に同一空間に行と列の要素をプロットできるNishisato and Clavel(2003)の提案がなされています。
Greenacre（1994）は行スコアと列スコアを一つの空間に重ね書きすること（overlaying plotとかjoint displayあるいはFrench plotとも呼ばれる）は解釈に便利だとしています。しかし彼自身が”the optimal display of the row profiles and of the column profiles, even though these sets of points occupy different spaces”と述べていて、２つの空間が異なることを認めています(Greenacre ,1994, p.21)。
そこで当面のところ、岩坪(1987,p118)がしているように行要素と列要素を別々の散布図に書くというグラフィック表現が手堅い対応でしょう。朝野（2010）は実務におけるグラフィック表現のDOs とDON’Tsを詳細に論じています。
もう一つの方針は、厳密でないことは承知した上で重ね書きする、という対応もあります。仮にプロットをクラスター分析するにしても、ブランドはブランドだけでクラスター分析をし、イメージ変数はイメージ変数だけでクラスター分析すればよい。ブランドとイメージ変数を一緒にクラスター分析しなければ実害はないだろう、というものです。マーケティングの実務では後者の対応がしばしばみられます。
3.終わりに
低次元でありながらも原データの情報が再現できる２相点間距離が定義できないかというのが、1990年ごろの私の関心事でした。それは無茶な相談だというのが最近の西里（2014）の見解です。結局空間の次元を拡張するしかない、という見通しです。西里先生はまた、本来は複雑なデータ構造にもかかわらず、低次元の解釈だけで済ませることを戒めています。たしかに因子分析で30因子も抽出しておきながら、最初の２ないし３因子だけを図示して済ませてしまうデータ解析を目にすることがありますね。
また西里先生は原データを名義尺度と扱ってデータ解析することこそ正しいアプローチであり、リッカート尺度のようにいいかげんな得点を与えてデータ解析をするのは誤りだ、とも指摘されています。私は原データが順序尺度なら順序尺度としてデータ解析をすればよいのであって、わざわざ名義尺度までdown-gradeすることはないと考えています。そのために例えばコンジョイント分析が開発されたのではないでしょうか。
しかし、一般的にいって名義尺度と順序尺度を明確に区別したデータ解析が貧弱であって、実数データの解析と比べると立ち遅れていることは否めません。
特にマーケティングで必要になる低水準尺度の解析法がなかなか進歩しないことは、いわばメーカーにあたる統計学者に対する我々ユーザーの要望発信力が足りないことの証左でしょう。自戒をこめて本エッセーを終えたいと思います。ここまで読んで下さった読者の皆様に感謝します。
引用文献
朝野熙彦（1974）多変量解析の論理的拡張について、消費研究,Vol 9, No.1, 1-20.
朝野熙彦（2008）コレスポンデンス分析の空間表現－PSVDの提案－.マーケティング・リサーチャー,No.107, 43-53.
朝野熙彦（2010）「最新マーケティング・サイエンスの基礎」講談社
Benzecri,J.P.(1973) Pratique de L’Analyse des Donnees ( Tom 2). Paris:Dunod.
Carroll, J.D.,Green, P.E. and Schaffer, C.M. (1986) Interpoint distance comparisons in correspondence analysis. Journal of Marketing Research, Vol.23,271-280.
Gifi,A. (1990) Nonlinear Multivariate Analysis. John Wiley & Sons.
Greenacre,M.J. (1994) Correspondence analysis and its interpretation. In Greenacre,M.J. and Blasius,J.(eds) Correspondence Analysis in the Social Sciences. Academic Press.pp3-22.
Guttman,L.(1941) The quantification of a class of attributes: A theory and method of scale construction. In Horst,P.,et al., The Prediction of Personal Adjustment. Social Science Research Council,319-348.
Hayashi,C.(1952) On the prediction of phenomena from qualitative data and the quantification of qualitative data from the mathematico- statistical point of view. Annals of the Institute of Statistical Mathematics, Vol.3,No.2,69-98.
岩坪秀一（1987）「数量化法の基礎」朝倉書店
Mosteller,F.(1949) A theory of scalogram analysis, using noncumulative types of items: A new approach to Thurstone's method of scaling attitudes. Rep.No.9, Lab.of Soc.Relations, Harvard University Press.Nishisato,S. and Clavel,J.G.(2003) A note on between-set distances in dual scaling and correspondence analysis, Behaviometrika, Vol.30,No.1,87-98.
Nishisato, S.(2007) Multidimensional Nonlinear Descriptive Analysis. Chapman & Hall/CRC,98.
西里静彦（2014）行動科学への数理の応用：探索的データ解析と測度の関係の理解、行動計量学、41,(2)、89-102.
Shiba,S.（1965a) The method for scoring multicategory items. Jap.Psychol. Res.,Vol.7,75-79.
Shiba,S.（1965b) The generalized method for principal components of scale analysis. Jap.Psychol. Res.,Vol.7,163-165.
竹内啓・柳井晴夫（1983）「多変量解析の基礎」東洋経済新報社
柳井晴夫（1994）「多変量データ解析法－理論と応用」朝倉書店
付録
data z; /* コレスポンデンス分析とその後の距離計算 */
input id$ y1 y2 y3;
cards ;
A 1 1 2
B 0.0 3 1
C 2 2 4
D 1 0.0 3
;
run;
proc iml ;
use z ;
read all var _num_ into z[ colname = vars rowname = id ] ;
/*----------------行列の規準化------------------*/
p = nrow( z ) ; /* 行数 */
q = ncol( z ) ; /* 列数 */
if p <= q then t = p ;
else t = q ; /* 空間の最大次元数 */
r = diag( z[,+] ) ; /* 行和の対 角行列 */
c = diag( z[+,] ) ; /* 列和の対角行列 */
rs = inv( sqrt( r ) ) ;
cs = inv( sqrt( c ) ) ;
x = rs * z * cs ; /* Ｚを規準化した行列Ｘ */
reset noname ;
call svd( u, l, v, x ) ; /* Ｘの特異値分解 */
a = rs * u * diag( l ) ; /* ブランド・スコア行列 */
b = cs * v * diag( l ) ; /* イメージ・スコア行列 */
print '原データ行列Ｚ' ;
print z[ format =10.0 ];
print '規準化データ行列Ｘ';
print x[ format = 10.3 ] ;
print l[ format = 15.3 colname = "特異値λ" ] ;
reset autoname ;
a3=a[ , 2:t ] ;
b3=b[ , 2:t ] ; /* 2:tとしてトリビアルな解を除去 */
print a3 [ colname = "ブランド・スコアＡ" format = 10.3 ] ,,
b3 [ colname = "イメージ・スコアＢ" format = 10.3 ] ;
/*------------------ 行プロフィールの準備 -------------------*/
aa = a3 * a3` ;
f = inv( r ) * z * cs ;
ff = f * f` ;
/*------------------ 列プロフィールの準備 -------------------*/
bb = b3 * b3` ;
g = rs * z * inv( c ) ;
gg = g` * g ;
/*------------------ ブランド空間内の距離 -------------------*/
j = j( p, 1, 1 ) ;
d1 = diag( ff ) * j*j` - 2 # ff + j*j` * diag( ff ) ;
d2 = diag( aa ) * j*j` - 2 # aa + j*j` * diag( aa ) ;
print "性質：行空間の点間距離の検討" ,,
"ブランドの点間距離", d2[ format = 10.3 ] ,,
"行プロフィールの行間の距離" , d1[ format = 10.3 ]
;
/*------------------ イメージ空間内の距離 -------------------*/
k = j( q, 1, 1 ) ;
d3 = diag( gg ) * k*k` - 2 # gg + k*k` * diag( gg ) ;
d4 = diag( bb ) * k*k` - 2 # bb + k*k` * diag( bb ) ;
print "性質：列空間の点間距離の検討" ,,
"イメージの点間距離",, d4[ format = 10.3 ] ,,
"列プロフィールの列間の距離" ,, d3[ format = 10.3 ]
;
reset autoname;
quit ;
